19.6. グラフの描き方
Mathematica では様々な種類のグラフを描くことができます。既にここまでの節の中でも何度か用いました。この節では色々なグラフを描いてみましょう。
関数 y=f(x) のグラフ #
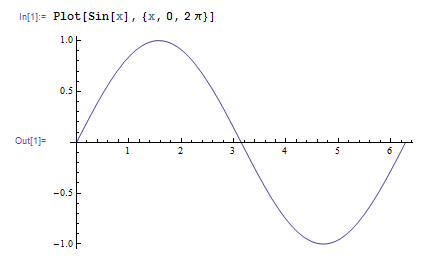
1 変数関数のグラフを描くには Plot 関数を使います。たとえば Plot[Sin[x], {x, 0, 2 Pi}] と入力して ![]()
![]() を押すと、1 周期分のサインカーブが描かれます。円周率は Pi と打っても、パレットから円周率ボタン
を押すと、1 周期分のサインカーブが描かれます。円周率は Pi と打っても、パレットから円周率ボタン で入力しても構いません。
で入力しても構いません。
関数を {F(x), G(x), … } のようにリストで与えると、全部のグラフをまとめて描いてくれます。たとえば Plot[{Sin[x], x, x – x3/6}, {x, -Pi, Pi}] と入力して ![]()
![]() を押すと、これらのグラフが同時に描かれます。
を押すと、これらのグラフが同時に描かれます。
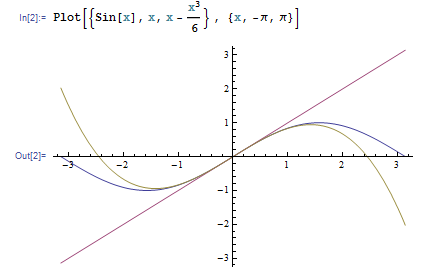
Plot 関数のオプションを指定することで、グラフの見栄えを調整できます。オプションの使い方については、このページの最後の項目を見てください。
パラメータ表示された曲線のグラフ #
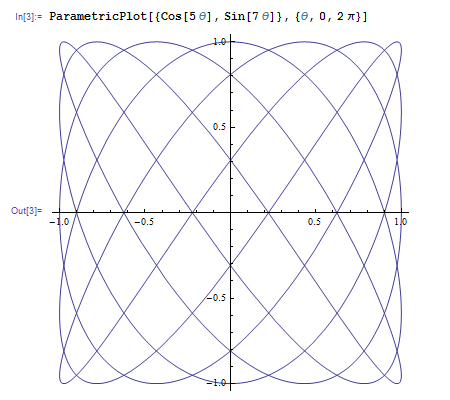
パラメータ表示された曲線を描くには ParametricPlot 関数を使います。x, y 座標を指定するだけで、あとは Plot 関数と全く同様に使えます。たとえば ParametricPlot[{Cos[5 θ], Sin[7 θ]} , {θ, 0, 2 Pi}] とすれば、Lissajous 曲線が現れます。Plot 関数と同様に {θ, 0, 2 Pi} は θ が 0 から 2 Pi まで動かすことを意味します。θ は基本数学アシスタントのパレットから入力できます。
陰関数表示された曲線のグラフ #
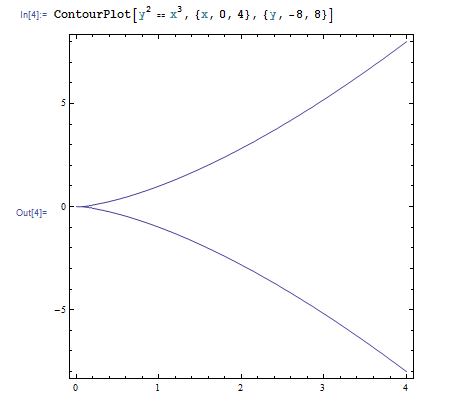
陰関数表示、すなわち F(x,y)=0 の形で定義される曲線を描くには ContourPlot 関数を使います。たとえば次のようにすると
\(y^2 = x^3\)
の曲線の原点付近での様子が描かれます。Mathematica では等号を == で表すことに注意してください。
極方程式で与えられた曲線のグラフ #
極方程式で与えられた曲線を描くには PolarPlot 関数を使います。たとえば r=1/(1+Cos[θ] /2) は楕円の極方程式です。このグラフを描かせてみましょう。
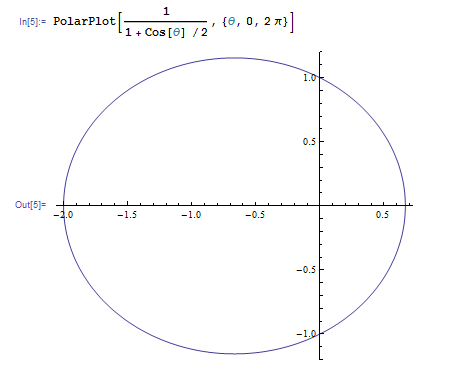
この式で Cos[θ] の係数は離心率と呼ばれ、離心率が 0 以上 1 未満の時は楕円、1 のときは放物線、そして 1 以上のときは双曲線になります。離心率を色々な値にしてグラフを描いてみてください。
リストデータのプロットと対数プロット #
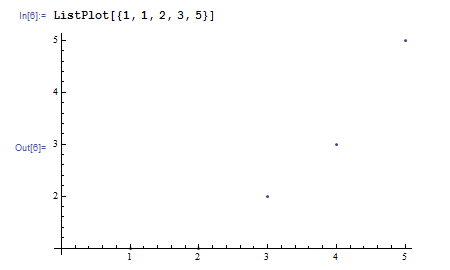
リスト形式で与えられたデータをプロットするときは ListPlot 関数を使います。たとえば ListPlot[{1, 1, 2, 3, 5}] とすると、x=1, 2, 3, 4, 5 のところにそれぞれ 1, 1, 2, 3, 5 がプロットされます。
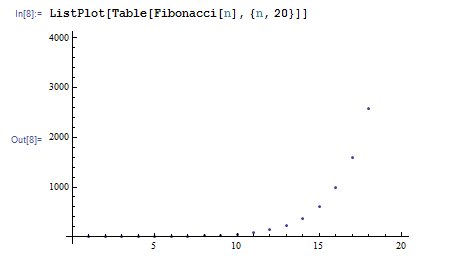
Table[Fibonacci[n], {n, 20}] とすると、Fibonacci 数列の最初の 20 項がリスト形式で得られます。

これをプロットすると、Fibonacci 数列の増え方が見えます。
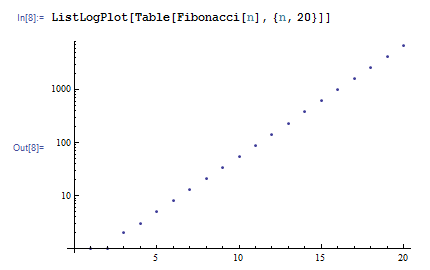
ListLogPlot 関数を使うと片対数グラフを、ListLogLogPlot 関数を使うと両対数グラフを描くことが出来ます。対数グラフがよく使われる場面として、巾乗則に従うデータのプロットがあります。たとえば今描いた Fibonacci 数列のグラフを片対数でプロットすると、直線が見えます。
また次の例では、y=x3 の区間 [0,1] での積分を台形公式で近似したときの誤差を計算しています。
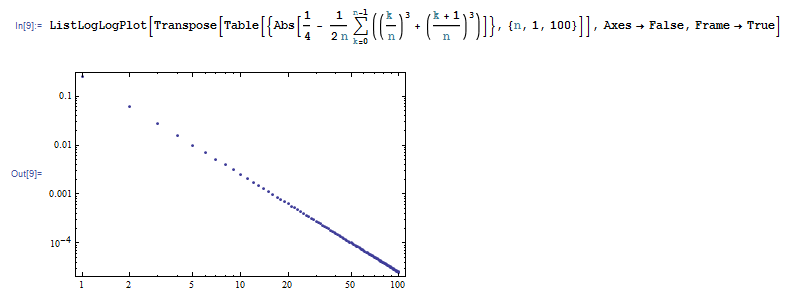
区間 [0,1] を等間隔に区切るとき、台形公式の誤差は分点数の (-2) 乗に比例します。この事実を反映して、両対数グラフを描くと直線が現れます。
領域の塗りつぶし #
RegionPlot 関数を使うと、不等式で定義された領域を塗りつぶすことができます。たとえば次の例では、x 座標が -3 から 3、y 座標が 0 から 2 の範囲で、 \(y \le \text{Exp}(-x^2/2)\) を満たす領域を塗りつぶしています。
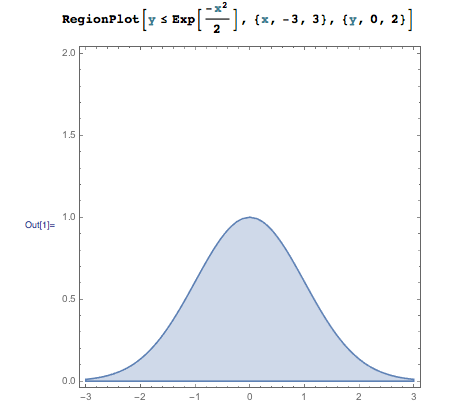
また、条件を && という記号で組み合わせることもできます。上の例と枠の領域は揃えたままで、
\(x \ge -2\)
かつ
\(x\le2 \)
という条件を組み合わせると、領域の両端がカットされます。
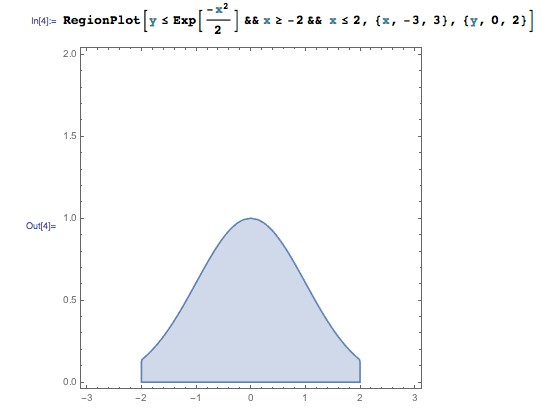
平面上の関数 z=f(x,y) のグラフ #
平面上の関数のグラフを描くには Plot3D 関数を使います。平面上の関数ですから、描く領域を指定する際に x 軸の範囲と y 軸の範囲を両方指定する必要があります。たとえば \(x^2-y^2\) のグラフを描くと、原点が鞍点になっていることが分かります。
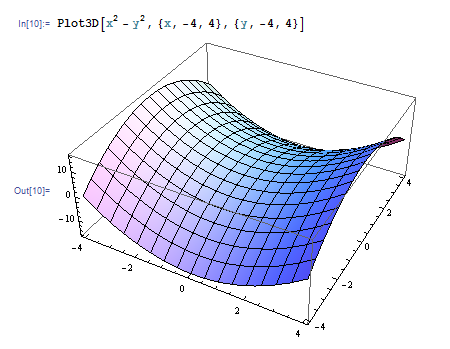
マウスでグラフをドラッグすると視点の変更をすることができます。はいぱーワークブック内ではお見せできませんので、各自 Mathematica で試してみてください。
陰関数表示された曲面のグラフ #
陰関数表示された曲面を描くには ContourPlot3D 関数を使います。たとえば ContourPlot3D[x^2 + y^2 – z^2 == 1, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}] で一葉双曲面が描かれます。
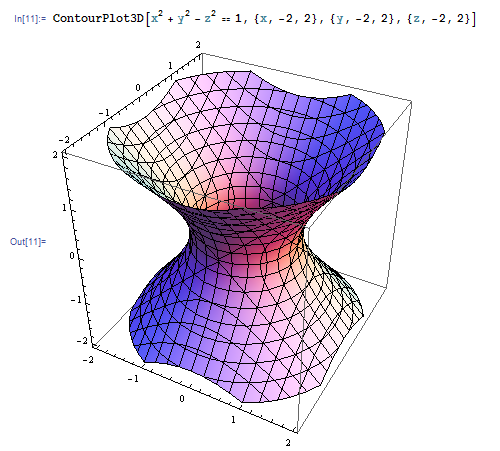
パラメータ表示された曲面と曲線のグラフ #
3 次元空間内でパラメータ付けられた曲線と曲面を描くときは ParametricPlot3D 関数を使います。この関数は曲線と曲面の両方に適用することができます。たとえば次の例では 2 次元トーラスを描いています。
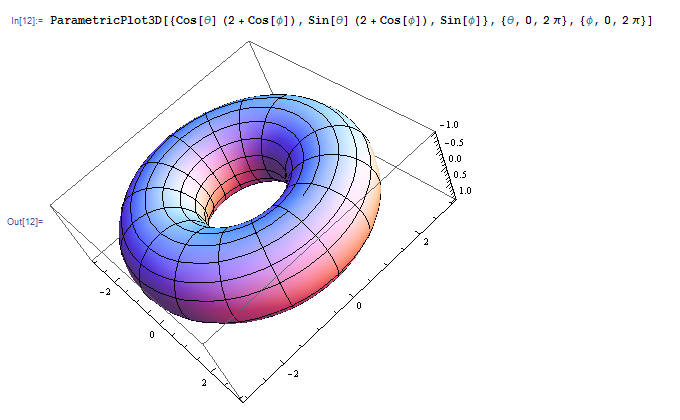
Cos[[θ] (2 + Cos[φ]), Sin[θ] (2 + Cos[φ]), Sin[φ] の 3 つがそれぞれ x 座標、y 座標、z 座標を与える関数です。 \(\{\theta, 0, 2 \pi\}\) と \(\{\varphi, 0, 2\pi\}\) でそれぞれ θ と π の動く範囲を指定しています。
また次の例では、 \(x=t^2, y=t^3, z=t\) で表される 3 次元空間内の曲線を描いています。パラメータの数が違う以外は、曲面の描き方と全く同じです。
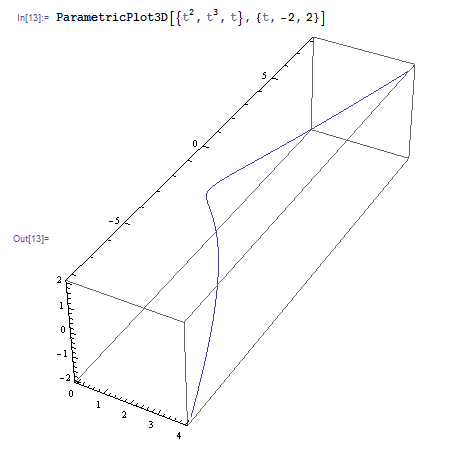
この曲線は ContourPlot の例で用いた曲線 \(y^2 = x^3\) の原点におけるブローアップと呼ばれます。パラメータ表示からも分かりますが、z 軸の正の方向からのぞき込むと \(y^2 = x^3\) が見えます。
グラフの重ね合わせ #
異なる種類のグラフを重ね合わせるには Show 関数を使います。たとえばShow[ContourPlot[y^2 == x^2 (x + 1), {x, -1, 1}, {y, -1, 1}], Plot[x, {x, -1, 1}, PlotStyle -> Red]] とすると、曲線 \(y^2=x^2 (x+1)\) と y=x のグラフが同時に表示されます。
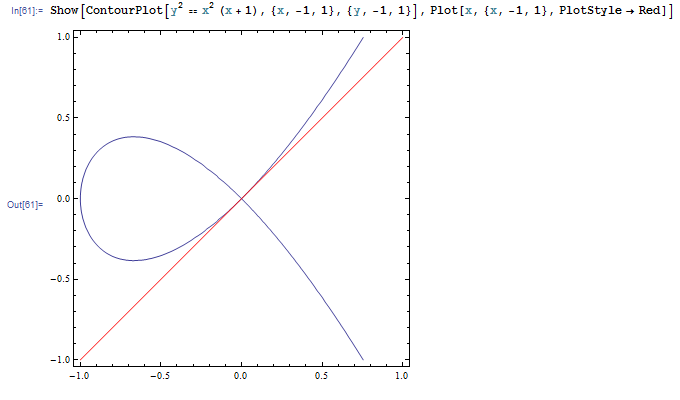
3 次元グラフ同士の重ね合わせもできます。たとえば次の例では、上で描いた 2 次元トーラスと平面 x=1 を重ねて描いています。断面の様子を見やすくするため、ParametricPlot3D にいくつかオプションをつけています。
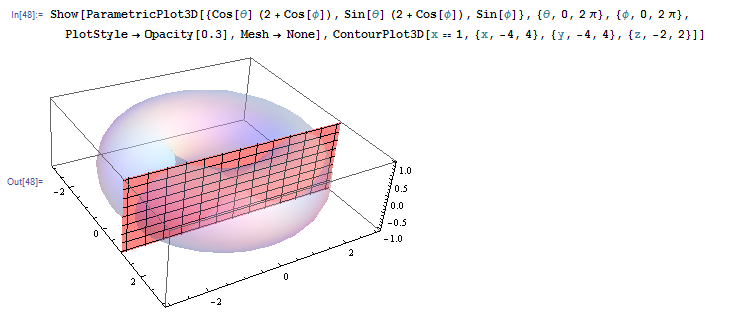
実は、この断面はレムニスケートです。
グラフ描画のオプション #
Plot 系の関数では、オプションを指定することでグラフの見栄えを色々調整することができます。いくつかオプションを使ってみましょう。Plot 系の関数ならどれでもほとんど同じオプションを設定できるので、以下の説明では Plot 関数を使うことにします。
まず次の図のように Frame -> True と指定すると、枠が描けます。
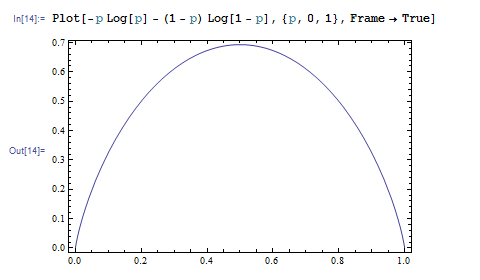
軸の有無は Axes オプションで設定できます。Axes->False と指定してグラフを描くと、軸が消えます。
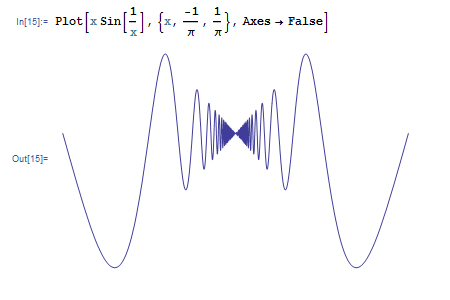
Axes->{True, False} とすれば y 軸だけが消えます。逆に {False, True} とすれば x 軸だけが消えます。
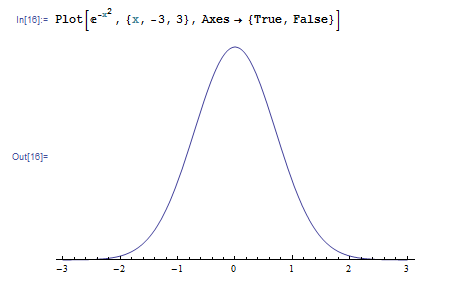
軸のラベルを設定するには AxesLabel オプションを指定します。
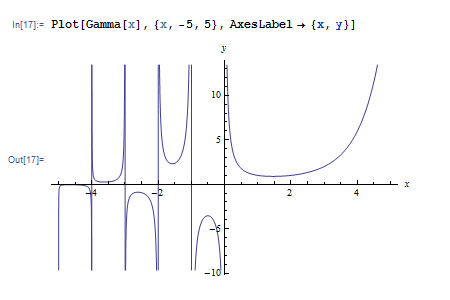
Plot 関数はグラフを描く領域を自動で判定してくれますが、明示的に指定したい場合は PlotRange オプションを使います。
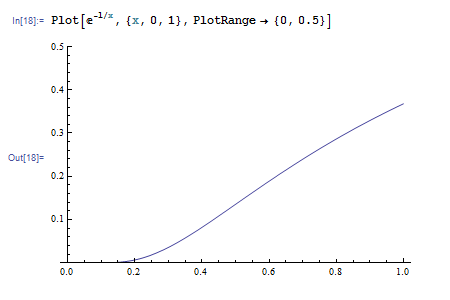
プロットする線の形状や色を変えるには PlotStyle オプションを指定します。たとえば PlotStyle->Red とすると、赤色でグラフが描かれます。
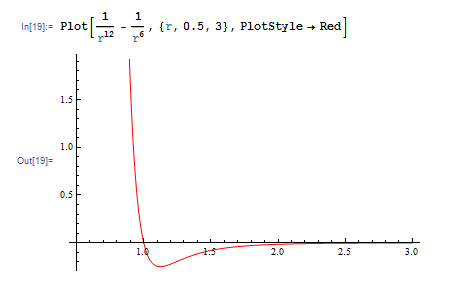
線種も指定することができます。PlotStyle->Dashed とすると、点線でグラフが描かれます。
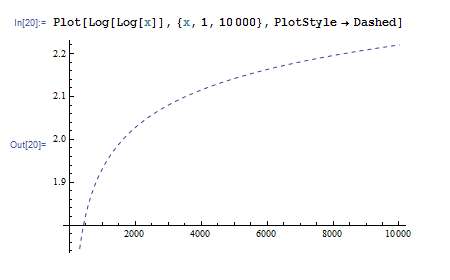
これらのオプションを同時に指定するには Directive という指示子を使います。
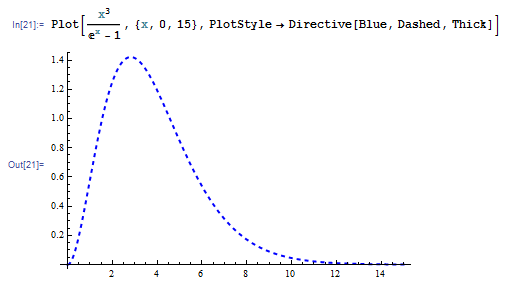
複数のグラフを同時に描く場合でも、それぞれのグラフに対して PlotStyle を指定することができます。次の例では x 以下の素数の個数を与える PrimePi 関数と x/Log[x] のグラフを同時に描いています。前者が青くて太い実線、後者が赤い点線です。
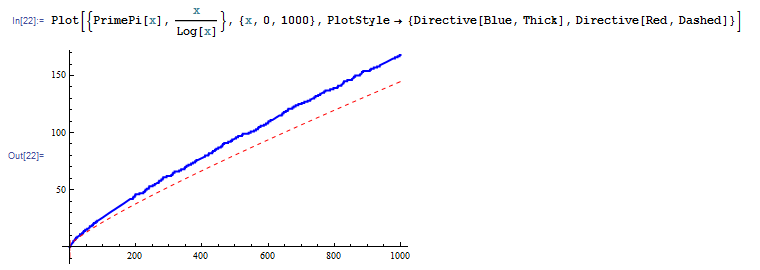
その他のオプション一覧を見るには Options[Plot] と入力します。

この通り、Plot 関数には実にたくさんのオプションがあります。ここで紹介できなかったオプションの使い方は、各自で調べてください。