18.9. リストの使い方とプログラミング
Mathematica を使う上で要になるのがリスト構造です。リストを使うことによって Mathematica でできる作業の幅が一気に広がります。またループや条件分岐を使うと、Mathematica で複雑な操作を行うことができます。この節ではリストと制御構造の使い方を説明します。
リストの生成と操作 #
リストを定義する一つの方法は、リストの内容を列挙することです。たとえば L={1,2,4,8,15} と入力して
を押すと、リスト L が右辺で定義されます。リストには中かっこ {} を使います。
リストの成分を取り出すには二重の角かっこ [[ ]] を使います。これはキーボードで二重に [[ ]] を打ってもよいし、あるいはパレットの二重括弧ボタンを押しても構いません。たとえば L[[3]] と入力すると 4 が帰ってきます。
関数によってはリストを返してくるものがあります。たとえば RandomInteger 関数は与えられた範囲の整数を指定された個数だけランダムに選び、順番にリストに入れて返します。
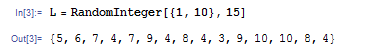
リストの末尾に要素を付け加えるには AppendTo 関数を使います。
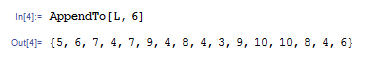
Reverse 関数を使うと、順序を逆にしたリストが帰ってきます。
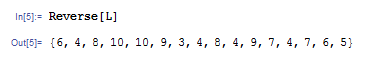
Sort 関数を使うと、リストの内容が適当な順序で整列されます。
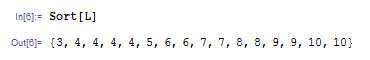
なお Reverse[L], Sort[L] を行ってもリスト L そのものは変化しません。実際に L と入力したあと
を押し、確認してみてください。
リストの要素を数えるには Count 関数を使います。
関数の値のリストを作りたいときは Table 関数を使います。たとえば Table[n2+n+41, {n, 0, 40}] と入力すると、n2+n+41 に n=0, 1, … , 40 を代入してできる値のリストができます。
Map 関数を使うと、リストの各要素に対して一斉に関数を適用できます。たとえば PrimeQ 関数は与えられた整数が素数であるかどうか判定する関数です。これを今作った n2+n+41 の値のリストに施すと、出てきた数が最後の1個を除き全て素数だと分かります。実際 1681=412 は素数ではありません。
Mathematica では、行列は「リストのリスト」として実装されています。たとえば {{1, 2}, {3, 4}} は左上・右上・左下・右下の順に 1, 2, 3, 4 を並べた 2 次正方行列を表し、 18.5. 行列の計算 で説明したパレットでの入力と全く同じ意味になります。実際 MatrixForm で表示させると、行列の形になります。
もちろん「リストのリスト」のリストなども作ることができます。これを応用すれば、テンソル計算もできますね (足の上下は自分で考えないといけませんが)。
条件分岐 #
条件分岐には If 文を使います。たとえば F[x_]=If[x<=0, -1, 1] と入力して
を押すと x<=0 のときは -1, そうでないときは 1 を返す関数 F ができます。If の中に順番に条件、条件が満たされたときに返す値、満たされなかった時に返す値を書くわけです。
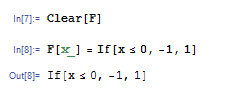
期待を満たす挙動をしているかは、Plot 関数でグラフを描いてみれば分かります。
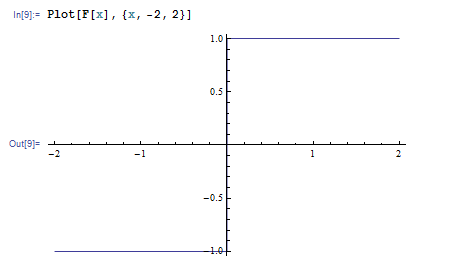
他にも条件文として Switch 文と Which 文が使えますが、以下の例で使わないのでここでは説明しません。必要に応じて各自で調べてください。
ループ #
ループ構文の例として For ループの使い方を説明します。この他に Do ループと While ループがありますが、これらの使い方は各自で調べてください。
For ループの使用例を一つ挙げます。たとえば For[ i=0, i<5, i++, Print[i]] とすると 0, 1, 2, 3, 4 が順番に表示されます。
この例から分かるように、上の For 文は「最初に i=0 とし」「i<5 が成り立つ間」「Print[i] を実行し」「1 ステップごとに i++ する」と読みます。i++ は「i に i+1 を代入する」という意味です。また0から 4 が表示されているので、Print[i] が i++ より先に実行されていることが分かります。この順序には気をつけておきましょう。
For には入力するものが 4 つありますが、これらの欄にはセミコロンを区切って複数の文を入力することができます。たとえば
For[x = 0; y = 0, Abs[y – Cos[y]] >= 0.01, x = y; y = Cos[y], AppendTo[L, {x, y}]; AppendTo[L, {y, y}]]
とすると
- まず x=0, y=0 とし
- y-Cos[y] の絶対値が 0.01 より大きければ
- リスト L に {x,y} と {y,y} を順に加え
- x=y, y=Cos[y] を代入して手順 2 に戻る
というようになります。最初に L を空にしてから上の文を実行すると、0 に Cos を何回も施したものがリスト L に入っていることが分かります。
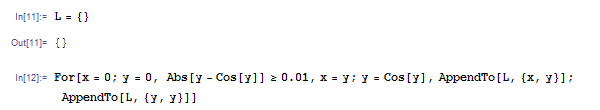
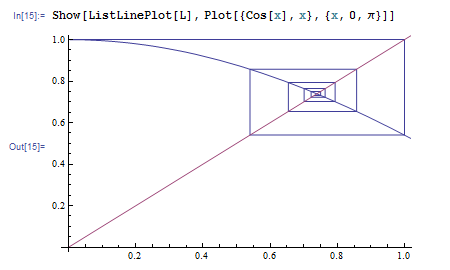
ListLinePlot[L] をすると、L に属する点を順番につないでできるグラフが表示されます。
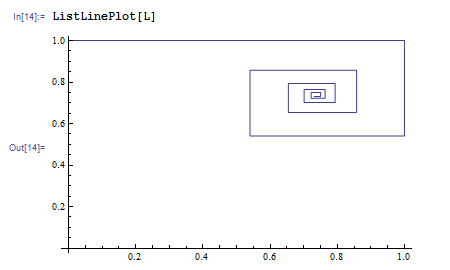
何をやっているのかと思うでしょうが、リスト L を点の列だと思って ListLinePlot をし、このグラフと Cos[x], x のグラフを重ねて描けば意味が分かります。
応用例: 擬素数の発見 #
リストと制御構造の応用例として、擬素数探しをしてみましょう。
素数を確率的に判定する方法の一つに Fermat テストというものがあります。Fermat テストのベースになるのは Fermat の小定理です。 \(p\) を素数、 \(a\) を \(p\) と互いに素な自然数とするとき、 \(a^{p-1}\) は \(\text{mod } p\) で1と合同になります。Mathematica で実験してみましょう。PowerMod[a,b,c] は a の b 乗を mod c で計算する関数です。たとえば a=15, p=7 の場合、PowerMod[15,6,7] を計算すると確かに 1 が帰ってきます。
PowerMod 関数を使わず、15 の 6 乗を実際に 7 で割っても同じ結果が確認できます。
この対偶を取ると「 \(p\) と互いに素な整数 \(a\) について \(a^{p-1}\) \(\text{mod } p\) が \(1\) でなければ、 \(p\) が合成数である」となります。もちろん \(a^{p-1} \text{ mod } p = 1\) だからといって \(p\) が素数だと言えるわけではありません。しかし \(a\) を色々取り替えてもこの式の値が全部 \(1\) になれば、 \(p\) が素数である可能性が比較的高いと言うことができます。このようにして確率的に素数を判定する方法を Fermat テストと言います。二つの整数か互いに素であるかどうかは Euclid の互除法を使えば高速に計算でき、また PowerMod 関数も高速です。Fermat テストは地道に素数判定をするより圧倒的に早く素数にあたりをつけることができます。
ためしに、501 以上 600 以下の整数について p=7, 13, 19 で Fermat テストをしてみましょう。まずはリスト L に 501 以上 600 以下の整数を格納し、PrimeList を 7, 13, 19 と定義します。
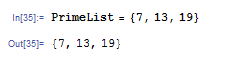
そして 1 を 100 個並べた IsPrime というリストを用意します。このリストは素数判定のフラグに使います。
実際に素数判定を行うのが次の文です。
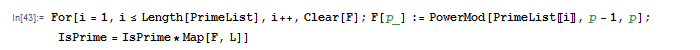
この文の内容を読み解いてみましょう。
- Length[PrimeList] は PrimeList の長さを表します。なので i は 1 から PrimeList の長さまでの整数を動きます。
- Clear[F] で関数 F をクリアしたあと F[p_] := PowerMod[PrimeList[[i]], p – 1, p] で F を定義し直しています。F[p] は a=PrimeList[[i]] に対して \(a^{p-1} \text{ mod } p\) を計算する関数です。
- Map[F,L] でリスト L の要素全てに F を適用し、そうしてできるリストを IsPrime と各成分ごとに掛け合わせます。F を施して 1 以外の値が出れば合成数なので、この操作の後に IsPrime の成分で 1 になっていないところを調べると、対応するLの要素は確実に合成数と言えます。
IsPrime を表示させると次のようになります。
IsPrime が 1 になっている場所を調べ、そこが本当に素数になっているかを調べます。すると一つだけ素数でない数が混ざっています。
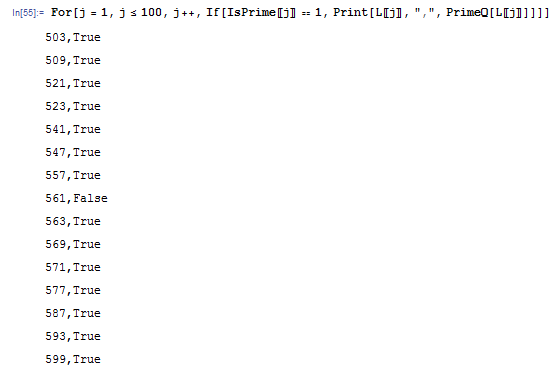
\(561=3\cdot 11\cdot 17\) なので確かに 561 は素数でありません。このように Fermat テストを通過してしまう数を擬素数といいます。特に 561 は自分と互いに素な全ての自然数に対する Fermat テストに合格するという性質があり、このような数は Carmichael 数とか強擬素数と呼ばれます。
こうして擬素数が見つかりましたが、上のプログラムは説明につかうためという目的もあり、決して洗練されていません。興味のある方はソースを整理したり、あるいは拡張を試みられると良いでしょう。