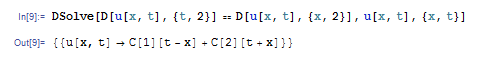18.8. 方程式を解く
Mathematica を使うと方程式を解くこともできます。この節では、代数方程式と微分方程式を解く方法を説明します。
代数方程式 #
代数方程式を解くには Solve 関数を使います。たとえば Solve[x2-3x+2 == 0 , x] と入力して
を押すと、2 次方程式
\(x^2-3x+2=0\)
を
\(x\)
について解いてくれます。等号を == で表すことにだけ気をつけてください。
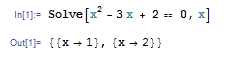
このように、Solve 関数は解きたい方程式系と変数を指定して使います。方程式系は1本だけである必要はなく、連立させる方程式を && で区切って並べれば連立方程式も解けます。たとえば \(x^2+y^2 = 1\) と \(y = x/\sqrt{3}\) を連立させて解くには、次のようにします。
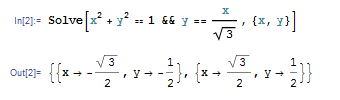
方程式の本数が少ないときは、解が唯一に定まらないことがあります。例えば \(x+y=2\) と \(y+z=3\) を連立すると、その解は 3 次元空間内の 2 枚の平面が交わってできる直線です。よって解は 1 個のパラメータを用いて表示されます。このような場合、Mathematica はパラメータを含んだ式を出力します。
いくら Mathematica と言えど、代数的でない方程式は一般には解けません。たとえばグラフを描けば分かりますが、方程式 \(x=\cos x\) は区間 \([0, \pi]\) 内に唯一の解を持ちます。
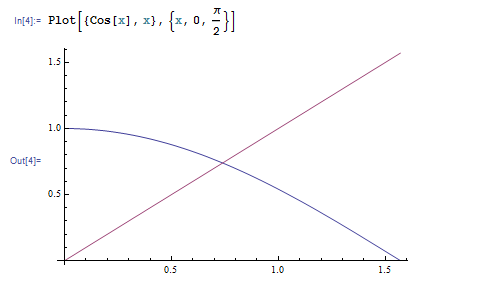
しかし Cos は代数的な関数でないから、この方程式を代数的に解くことはできません。Solve 関数を使うと解けないと言われてしまいます。
この場合は FindRoot 関数を使うと、解の近似値を計算できます。FindRoot[Cos[x]==x, {x, 0}] とすると、x=0 を初期値として解の探索が行われます。
微分方程式 #
微分方程式を解くには DSolve 関数を使います。たとえば単振動の方程式
\(y''=-k^2 y\)
の一般解は Sin[kx] と Cos[kx] の重ね合わせです。この方程式を Mathematica で解くには DSolve[y''[x]== -k^2 y[x], y[x], x] と入力して
を押します。すると任意定数 C[1], C[2] を含む解が得られます。
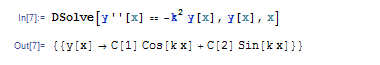
第 1 引数には解きたい方程式、第 2 引数には未知関数、そして第 3 引数には変数を入力するわけです。また初期条件を指定することもできます。たとえば微分方程式
\(y'=y\)
を初期条件 y[0]=1 のもとで解くには DSolve の第 1 引数を y'[x]==y[x] && y[0]==1 とします。
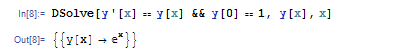
すると解である Exp[x] が表示されます。このように && で区切って式を並べると、それらを全て満たす解が表示されます。ですので、連立微分方程式を解くこともできます。
変数の数を増やせば偏微分方程式になります。偏微分方程式が解けることは多くないですが、熱、波動や Laplace などの基本的な偏微分方程式は解くことが出来ます。たとえば波動方程式を解くには DSolve[D[u[x, t], {t, 2}]==D[u[x, t], {x, 2}], u[x, t], {x, t}] とします。すると任意関数を含む一般解が表示されます。
