14.5. 音の符号化
この節では音声データをどのように符号化するか、またアナログ情報をデジタル情報へと変換する方法について説明します。
音 #
音は空気の密度の振動、波です。連続な時間で変化し続ける量を厳密に記録することはできないので、人の耳に区別できる範囲で記録することを考えます。
レコードへの記録
標本化と量子化 #
波をディジタル表現で変換する、素直な方法は、離散的な代表点を記録することです。 下図は正弦波を、水平または鉛直な線分を使った折れ線グラフで近似した例です。4枚の図は、縦横のグリッドの細かさが異なり、折れ線グラフの細かさが異なります。 この折れ線グラフは、整数座標、つまり、ディジタルで表すことができます。
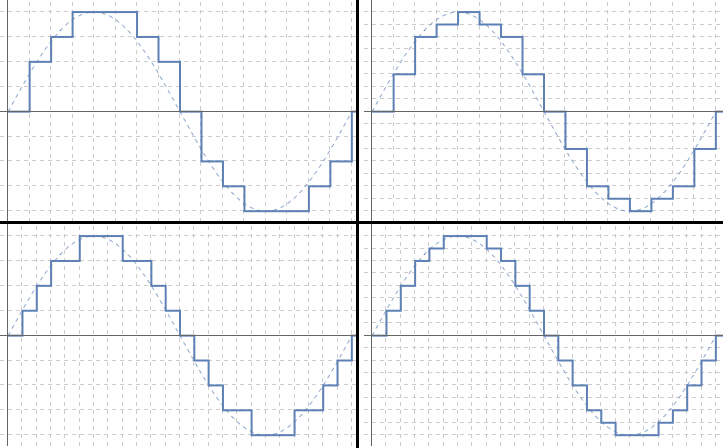
音の場合、横軸は時間軸で、一定時間毎にデータを記録することを 標本化(サンプリング) と呼びます。同様に 縦軸について振幅の刻み幅を設定して、離散値で表すことを 量子化 と呼びます。
具体例として、オーディオCD では、サンプリングレートが 44,100Hz、量子化ビット数 16 で記録されています。 前者は、1秒間に 4.41万回 記録する、後者は各記録を \(2^{16}=65536\) 段階に記録するという意味です。 それぞれの数値が大きいほど正確な表現になります。 また、等間隔で刻むよりデータに合わせて刻み幅を変えるような工夫も可能です。このような符号化を一般にPCM(パルス符号変調)方式と呼びます。
波と重なり #
自然界の音は、正弦波のような綺麗な形ではなく、複雑な形をしています。 そのような波も、さまざまな周期関数の重ね合わせの合成と理解することができます。
波を重ねる簡単な例は、sin関数の和です。 右図は大きな正弦波に、細かい正弦波を乗せたものです。
\(y = \sin (2\pi t) + 0.04 \sin (128 \pi t)\)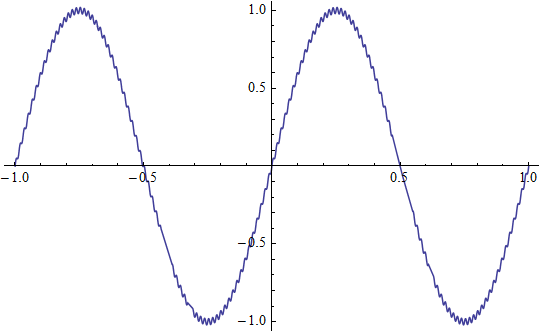
- 周期
- 周期的に同じ形を取る関数の、繰り返す単位を周期と呼びます。音なら時間で変化するので、0.1秒のように測ります。
- 周波数
- 周波数は単位時間に含まれる周期です。音の場合は単位時間を1秒として、周波数は
Hz(ヘルツ) で表現します。大きな値なら高い音、0に近い値なら低い音です。周波数の逆数が周期です。
Fourier 変換 #
合成とは逆に分解もできます。
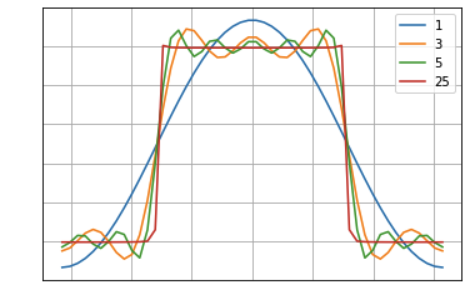
Fourier 変換は、波形をサインカーブの加算に分解する数学的手続きです。
分解後の個数が有限とは限りませんが、周期の長い順に先頭付近だけ使っても、元の波形にそこそこ近いグラフが得られます。
波形の周期 vs 標本化の間隔 #
波形を記録するのに必要な標本化の間隔は、記録したい波形がどの程度細かい周期関数を含むかで決まります。
もっとも単純なサインカーブを例に考えます。この関数の周期は 1 です。
\(y = \sin 2\pi t\)角度の単位にはラジアン (rad) を使います。
\(2\pi \text{ラジアン} = 360 \text{度}\)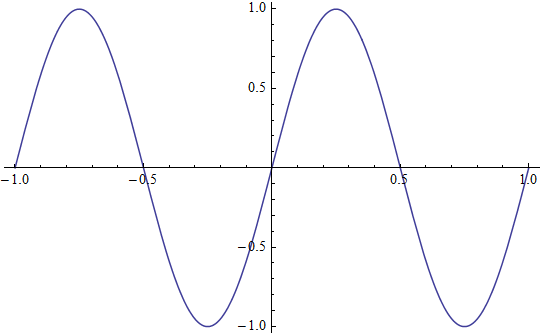
サンプリング間隔を 1/4, 1/8, 1/16, 1/32 と順次変えて標本化して、図にしました。

1/4 で標本化した絵だけを見ていても、元の波形を推測するのは難しいでしょう。一方 1/16 くらいの間隔で標本化したデータを見れば、かなり正確に元の波形を推測することができるはずです。1/32 まで細かくすれば、ほとんど元の波形が見えています。
- どの程度の周波数までの情報を拾う (必要がある) かを決め
- 拾うと決めた周波数の上限に対して、十分な標本化間隔を決める
という順番で標本化間隔を決めれば、元の波形がそれなりの精度で再現できます。
標本化定理 #
標本化定理は「波に含まれる周期関数の周波数の最大値があったら、その 2 倍の周波数以上で標本化すれば完全に再現できる」ことを主張します。 標本化定理を使う場合、標本化する周期から「何 Hz の波形までのデータを取れるか」を考えることも多いです。標本化する周期が \(T_0\) のとき、データの損失なしに標本化できる限界の周波数 \(1/T_0\) を Nyquist 周波数と呼びます。
音質 #
音楽 CD などでは、通常 44.1kHz でサンプリングが行わますが、これは妥当な数字でしょうか? 人間に聞こえる音には上限があり、それは大体 20000Hz = 20kHz と言われています。そして標本化定理によれば、サンプリングレートを 40kHz にすれば 20kHz 以下の音を損失無しに記録できます。この観点で、40kHz 程度のサンプリングをすれば人には考えられます。
このサンプリングレートでも、PCM で符号化された音声のデータは非常に大きくなります。
そこで可逆や非可逆の圧縮方法が開発されてきました。flac, m4a, mp3, aac などはその一例です。データ圧縮の形式や圧縮されたデータを利用するのに必要なプログラムやデータをコーデックと言います。
一番上の 44100Hz_16bit.wav は、サンプリングレート 44100Hz, 16bit 量子化による録音で作られています。
残りのファイルは 44100Hz_16bit.wav を加工してサンプリングレートを引き下げたものです。
| サンプリングレート | 量子化ビット | ファイルサイズ | |
|---|---|---|---|
| 44100Hz | 16bit | 4.5MB | |
| 32000Hz | 16bit | 3.3MB | |
| 22050Hz | 16bit | 2.3MB | |
| 16000Hz | 16bit | 1.6MB | |
| 11025Hz | 16bit | 1.1MB | |
| 08000Hz | 16bit | 844KB | |
| (mp3) | (mp3) | 797KB |
おそらく 44100Hz と 32000 Hz の間では、そこまで差を感じないのではないでしょうか?一方で 11025Hz や 8000Hz までサンプリングレートが下がると、音の劣化を認識できると思われます。 また最後のものは、320kbps で mp3 に圧縮したものです。大きさは減りましたが、音質の低下は抑えられています。