23.6. 統計に関する補足
統計処理をするときは、その意味をよく考える必要があります。表計算などの便利な道具ができたので「データ処理」だけは簡単にできますが、その適切な利用をするための学習も大切です。今回登場した統計量に関する補足を書いておきますので、一度目を通しておいてください。
主要な統計量 #
分散 #
いくつかの数値データが与えられたとき、それらの分散が「平均値との差の 2 乗」の平均値として定義されます。与えられたデータが x1, x2, …, xn で、これらの平均が m のとき、分散 V は
V = {(x1 – m)2 + (x2 – m)2 + … + (xn – m)2} / n
という式で与えられます。
分散はデータのばらつきの大きさを表す量です。たとえばデータが全部同じ値だとしましょう。このとき平均値も各データと同じ値なので x1 = x2 = … = xn = m です。これを分散の定義式に代入すると V = 0 が得られます。「データが全くばらつかないこと」が V = 0 と対応しています。また、今度はデータが 2 個しかない (つまり n = 2) としましょう。このとき平均は m = (x1 + x2)/2 なので、分散の式は
V = { ( (x1 – x2)/2 )2 + ( (x2 – x1)/2 )2 }/2 = (x1 – x2)2/4
となります。よって x1 と x2 の差が大きいほど、分散の値が大きくなることが分かります。確かに分散が、データのばらつきを測っていますね。一般の場合でも話は同じです。右辺に登場する項 (xk – m)^2 は常に 0 以上で、データ xk が平均 m から離れているほど大きい値を取ります。ですからデータのばらつきが大きいほど分散が大きくなります。
もしかしたら皆さんの中に「データのばらつきを測るなら、平均との差の 2 乗ではなく絶対値を考えても良いのではないか」と思った人がいるかもしれません。実際「平均との差の絶対値の平均」には平均偏差という名前がついています。ただ平均偏差が利用されることは稀です。この理由は、分散や標準偏差の方が平均偏差よりも良い性質を持つからだと思われます。特に
- 正規分布の形が、分散によって特徴づけられていること
- 後で紹介する中心極限定理を考える際、収束先の正規分布の分散が元々の分布の分散と一致すること
が決定的に重要です。残念ながら平均偏差は、こうした性質を持ち合わせていません。
標準偏差 #
標準偏差は分散の平方根として定義されます。つまり標準偏差を σ、分散を V とすると、σ2 = V です。分散も標準偏差も同じくデータのばらつき具合を表しますが、標準偏差には「元のデータと同じ単位を持つ」という特徴があります。ですので、たとえば「データが平均値とどれくらい離れているか」を測るときは、分散ではなく標準偏差をものさしに用います。
![]()
データの特徴を調べるときは、単に分散 / 標準偏差だけを見るのでは不十分です。これらの値は「ばらつき具合」しか測っていないので、ここから分布の山の個数などの特徴は読み取れません。ヒストグラムを描いて全体の分布の形を把握してから、ばらつき具合の評価をしましょう。
標本不偏分散 #
さて、データの平均や分散は「与えられたデータがどういう分布をしているか」を測る量でした。ですが実際にデータを観測する場面では、データが何らかの法則にしたがっているという仮定のもと、観測したデータ (標本、サンプル) からデータを生み出す分布を調べます。そのためには「独立かつ同じ分布に従う確率変数の標本があたえられたとき、それらの平均や分散などがどういう分布に従うか」を知らなければいけません。この「標本の関数の分布」のことを標本分布といいます。
実務上大事なのは、1 つ 1 つの標本が正規分布に従っている場合です。このとき、いくつかの標本から親玉の正規分布の平均や分散を知るには、どうすれば良いでしょうか?普通に考えると、標本の平均値や分散をそのまま使って親玉の分布を推定するのがよい気がします。ところが実は、親玉の分布の分散を推定する時は、平均からの差の 2 乗和をデータの個数で割るのではなく、(データの個数 – 1) で割らないと推定値が偏ってしまうことが知られています。このように (データの個数 -1) で割ってつくる分散を標本不偏分散といいます。
相関係数 #
2 つの系列を持つデータが与えられたとき、系列間の関係を相関といいます。
例えば色々な人について身長と体重を調べたとすると、一般には身長が高い方が体重も大きいはずです。このように関連が見られることを指して、2 つのデータは相関が強いといいます。これに対して視力と体重を比較すると、視力がよい方が体重も大きいと言えるでしょうか?おそらく、ほとんど無関係であることが予想されます。このように、一方のデータを見ても他方のデータを推測することがほとんどできないとき、2 つのデータは相関が弱いといいます。
また相関の強さとは別に、相関には正負の符号があります。「身長と体重」のように片方の値が大きいほどもう片方の値も大きくなる場合「正の相関」があるといい、「視力と眼鏡の所有数」のように反対の関係になっている時「負の相関」があるといいます。
こ のようなデータの組の相関の度合いを表す統計量として (Pearson の) 相関係数がしばしば用いられます。与えられたデータが (x1, y1), (x2, y2), …, (xn, yn) のとき、x だけの平均と標準偏差をそれぞれ mx, σx で、y だけの平均と標準偏差をそれぞれ mx と my で表すことにします。このとき、それぞれのデータについて x, y の値を標準化してかけたもの
{(xi – mx) / σx}{(yi – my) / σy}
を i = 1, 2, …, n について平均したものが、相関係数です。
相関係数は -1 から 1 までの値をとることが証明されます。相関係数の符号が相関の正負に、絶対値が相関の強さに対応しています。2 つのデータが完全に相関するとき、相関係数の絶対値は 1 です。
正規分布 #
正規分布は、統計に登場する分布のなかで最も重要な確率分布です。
- いわゆる「釣り鐘型」の分布であること
- 同じ分布に従う独立な確率変数がたくさんあったとき、それらの平均を標準化した確率変数の従う分布は、確率変数の個数が増えるほど正規分布に近づくこと (中心極限定理)
は、知っておいてください。ちなみに確率密度関数は exp{ (x – μ)2 / (2σ2) } / (2πσ2)1/2 で与えられます。
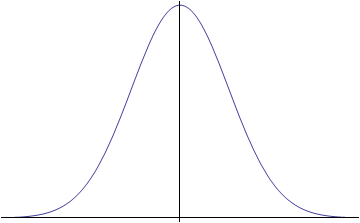
正規分布の場合には、釣り鐘型の真ん中が平均、釣り鐘型の広がり方が標準偏差で与えられます。(もう少し正確に言うと、グラフの変曲点が平均値 ± 標準偏差になっています。) そして正規分布では「平均値 − 標準偏差」から「平均値 + 標準偏差」の範囲内に全データのおよそ 68% が含まれるという性質があります。