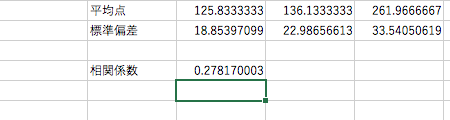
23.2.10. 簡単な統計処理
もう少し Excel の関数を使ってみましょう。前節で扱った AVERAGE 関数と SUM 関数に関連して、いくつかの統計量を計算する関数を紹介します。
なお、この節の主たる目的は Excel の関数に慣れ親しむことです。ですから統計的な説明は 23.6. 統計に関する補足 に回して、まずは関数を使ってみることにします。
このページでは 23.2.9. 関数の利用例 で作ったファイルを使います。まだ作っていない人は score_total_for_23_2_10.xlsx をダウンロードしてください。
分散と標準偏差 (STDEV.P) #
データの特徴を調べるにあたり、平均と並んでよく使われるのが分散と標準偏差です。これらはいずれも、データのばらつき具合を表す統計量です。データの分散と標準偏差を計算するために、それぞれ VAR.P 関数と STDEV.P 関数が用意されています。
標準偏差と分散の間には「標準偏差の 2 乗 = 分散」という関係があるので、どちらを使っても得られる情報は同じです。ここでは標準偏差を求めてみます。セル D33 に「標準偏差」という見出しを打ち込んでから、E33 に =STDEV.P(E2:E31) と入力してください。
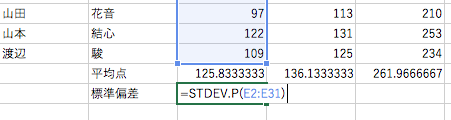
範囲指定のやり方は、これまでの AVERAGE 関数や SUM 関数のときと同じです。式の内容を
![]()
キーで確定させると、E33 に標準偏差の値が入力されます。

この式をコピーして隣のセル F33 にペーストすると、英語合計点の標準偏差が求まります。
![]()
「サンプルデータから真の値を推定する」というタイプの問題を考えるときは、標本分散と標本不偏分散という 2 種類の分散が登場します。この 2 つの違いは 23.6. 統計に関する補足 で説明しています。
Excel では、標本分散を VAR.P 関数、標本不偏分散を VAR.S 関数でそれぞれ計算します。単に VAR と書くと標本不偏分散 VAR.S が使われるようですが、標本分散と標本不偏分散の違いを意識するために VAR は使わず、VAR.P と VAR.S のみを区別して使うことをお勧めします。同様に、標準偏差にも 2 種類のものがあります。標本分散の平方根は関数 STDEV.P、標本不偏分散は関数 STDEV.S となります。また関数 STDEV は不偏な方 STDEV.S と同じですが、やはり使わない方が良いでしょう。状況に応じてその都度、STDEV.P と STDEV.S の適切な方を選択しましょう。
相関係数 (CORREL) #
相関係数とは「2 つのデータの間にどれくらい関連があるか」を表す指標です。Excel では CORREL 関数によって、相関係数の計算ができます。
ためしに、サンプルファイルの学生たちについて数学の成績と英語の成績の相関を計算してみましょう。適当なセル、たとえばセル D35 に「相関係数」と書き、その右のセル E35 に =CORREL(E2:E31,F2:F31) と入力してください。
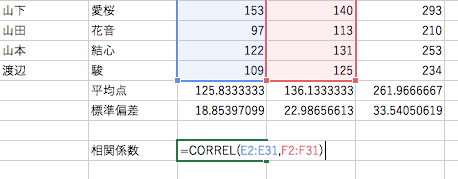
すると「数学の成績」と「英語の成績」の相関係数の値が求まります。