27.7 数式の書き方(1)

27.1 LaTeX についての概説 でも触れたように，TeX/LaTeX は数式を含んだ文章の作成に最初から重点がおかれて設計されています．本節では，主に数式記号の入力方法について説明します．

数式の基本

文章の中に埋め込まれた数式（文中数式）は，$ … $ と半角ドルで囲んで入力します．この $ … $ の中では，LaTeX は数式モードという特殊なモードになり，フォントも数式用のものに変わります．

• 数式モードの中では，半角空白は単に無視されます．
• 上添字・下添字はそれぞれ $x^2$, $a_n$ のように ^, _ を用います．二文字以上の添字を書くには $x^{10}$ と添字を {} で囲んでグループ化します．$a_{n^k}$ のように，「添字の添字」を入力することも可能です．
• 「f’」などのようなプライム記号（よく日本ではダッシュと呼びますが）は，単に f’ のように打って構いません．f”’^3_2 のように複数組み合わせることも，また上下添字と組み合わせることも可能です．
• 和の記号 Σ，積の記号 Π，積分記号 ∫ は，それぞれ \sum, \prod, \int を用います．和をとる範囲や積文範囲などは，添字の形で入力します．
• 分数は，\frac{分子}{分母} を使いますが，文中では 2/3 のようにスラッシュを使った割り算の形の方が良いでしょう．

また，独立した行に数式を書く場合は，\[ … \] を用いて表記します．これを別行立て数式といい，文中数式とは違った，より縦幅をとったスタイルで表示されることになります．
以下に，簡単な数式の例を挙げます：

文中の数式は$a<2$のように記述します．
$a>2$と$ a > 2 $のように，数式中の半角空白は単純に無視され，
$\sum_{i=1}^n i^2 = n(n+1)(2n+1)/6 = \frac{n(n+1)(2n+1)}{6}$,
$\prod_{i=1}^y i^3 =\int_0^1 f$のように，縦幅をとらない形になります．
別行立て数式は，
\[
 \sum_{i=1}^n i^2 = n(n+1)(2n+1)/6 = \frac{n(n+1)(2n+1)}{6}
\]
とか
\[
 \prod_{i=1}^y i^3 =\int_0^1 f
\]
のように，専用に行がとられます．

根号など

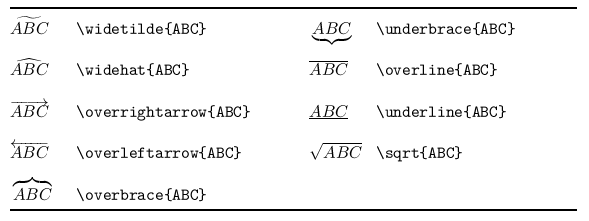
根号は \sqrt{ … } で出力します．これに類似したものに，次のコマンドがあります：

合同式で見かける a≡b (mod 3) などの表記や，省略を表す … は次のように入力します．\cdots と \ldots は上下位置が違うことに注意して下さい．

$a\equiv b \pmod 3$, \ $4\bmod 42$, \ $P(x_1,\ldots,x_n)$, \ $x_1+\cdots+x_n$

アクセント類

数式ではよくアクセント付きの記号が出てきますが，これらは本文とは違ったコマンドで出力します．

小文字の i, j に対してアクセントをつける場合， 27.3 文書の書き方 のときのように「上の点のない i, j」に対してアクセントをつけるのが普通です．このためには \imath, \jmath を使います．

ギリシャ文字と雑多な記号

まず，ギリシャ文字については，以下のコマンドを使います．ここに載っていないギリシャ文字（例えばアルファの大文字）は，普通の英語のアルファベットと形が同じなので，単にそちらを使います．
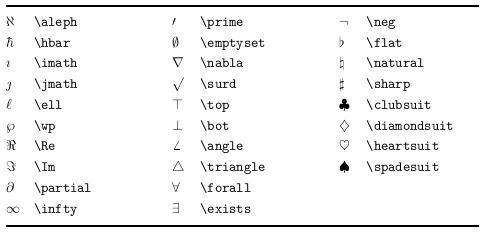
次に，「普通の文字」として扱われる雑多な記号です．面白いのはトランプのスペード・ハート・クラブ・ダイヤなども数式中の記号として用意されていることです：

大型演算子と log 型関数

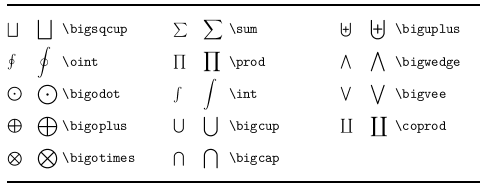
和を表す Σ などの記号は，文中数式と別行立て数式で組み方が変わります．以下の表では，左側が文中数式中の字形，右側が別行立て数式の字形を表しています：

また，log, sin, lim, max などの関数はそのまま

$ lim_{x\rightarrow\infty} 1/x $

のように書いてはいけません．このように書くと，l, i, m_{x\rightarrow\infty} という3変数の積だと LaTeX には解釈されます．代わりに，\lim などのコマンドを使います．

\[
 \lim_{x\rightarrow 0} \frac{\sin x}{x} = 1
  \neq lim_{x\rightarrow 0} \frac{sin x}{x}
\]

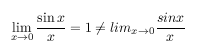
\lim などのコマンドは log 型関数などといわれ，以下のような種類があります．

二項演算子

次は +, – に代表される二項演算子です．

私たちは「-a」などのように，時々これらの記号を単項演算子として使うことをしますが，LaTeX でもその点は考慮されています．二項演算子として扱われたときと，単項演算子として扱われた時では，周囲の空きの入り方が異なったものになります．

単項演算子：$-a$, $(+d)$, $10.5+$
二項演算子：${}-a$, $b-a$, $a+d$
誤：$|-a|$（二項演算子）
正：$|{-a}|$（単項演算子）

関係演算子と矢印

等号や不等号などの関係演算子に類別されるものです．矢印もこの仲間にはいります．

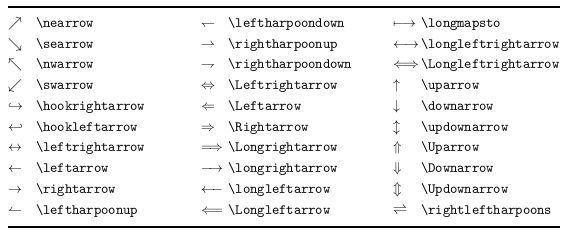
括弧類

以下に述べるのは括弧類です．括弧と言っても，「(」などの開き括弧と「)」などの閉じ括弧があり，さらに左右の区別がない括弧があります．左側は何も指定しない時の普通の大きさ，右側は大きくした形です：

上図右側のように，括弧を大きくするにはいくつかの方法があります．まずは手動で大きくする方法です．

• これら括弧類の直前に \big, \Big, \bigg, \Bigg コマンドを書くと，括弧が大きくなります．
• 開き括弧の場合には \bigl, \Bigl などと最後に l をつけたコマンドを使用します．
• 閉じ括弧の場合も，同様に \bigr, \Bigr のように最後に r をつけたコマンドを使用します．
• 関係を表す記号を大きくするには，\bigm, \Bigm のように最後に m をつけたコマンドを使用します．

括弧が入り組んだ数式を書く場合，これらのコマンドを用いて手動で調整してやることで，数式は格段に読み易くなります：

例1: $( \bigl( \Bigl( \biggl( \Biggl($
例2: $\bigl| |x|-|y| \bigr|$
例3: $A_x=\bigl\{\,y\in B \bigm| B\subset F(x)\,\bigr\}$
例4: $\bigl(x-g(x)\bigr)\big/ \bigl(y+h(x)\bigr)$
\[
 \int_0^1 (x^2+5x)\,dx
 = \biggl[\frac{x^3}{3}+\frac{5x^2}{2}\biggr]_0^1
 = \frac{17}{6}.
\]

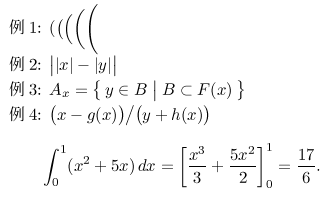
一方，中身に合わせて自動で括弧の大きさを調整することも可能です．この場合は，\left と \right  で囲みます．比較的最近の（例えば Windows 環境の） pLaTeX では \middle 命令も扱えるようになってきていますが，「一般的」とまでは言えないので説明はしません．

$(a^2_n)_n$, $\left(a^2_n\right)_n$, $A=\left]0,1\right]$←半開区間の1表記
\[
 \left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)f=0
\]
片方だけの括弧には，もう片方を \texttt{.} にすればよい．
\[
 \left( x^2 \right.
\]

\left, \right による自動調整は大半の場合によく動きますが，たまに適切なサイズにならない場合（括弧がネストしている場合など）があります．その場合は，面倒でも手動調整を行って下さい．

句読点扱い

細かいですが，以下は句読点扱いとなるものです．:（コロン）を句読点扱いにするには，\colon と入力する必要があることに気をつけて下さい．

数式中の書体

数式中でも，いくつかの書体を使うことができます．

以下の注意があります．

• 効用があるのは原則として英語の大文字・小文字，数字，ギリシャ文字の大文字だけです．
• 出力からもわかるように，複数文字からなる変数名などを書く時は \mathit を使った方が見栄えがよくなります．
• 筆記体を出力する \mathcal は，大文字しかでません．数字や英小文字の出力は変なことになっています．
• bm パッケージで提供されている \bm を使うと，記号類も太字にできます．

なお，数式中に直接 $和文$ のように書いて，和文文字を出力することもできます……が，それは意味的にも正しくない場合がほとんどなので，新しくソースを書く際にはそのようなことはしないで下さい．数式中に日本語を書く際には，原則として次節 27.8 数式の書き方(2) で説明する \text{ … } を使って下さい．また，古い pTeX だと，

$\hat あ$

でアクセントが異常になるというバグがあります．