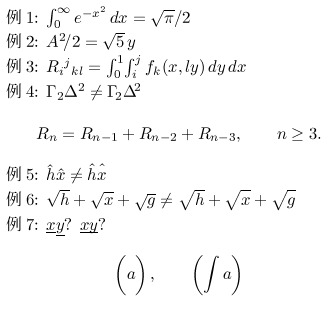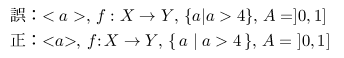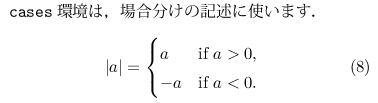27.8 数式の書き方(2)

前節 hwb27.7 数式の書き方(1) に引き続き，数式の書き方について更なる説明を行います．

空白の微調整

TeX/LaTeX は，自動でかなりのところ数式内の空きをうまく調整してくれますが，やはり手動で調整しないといけないようなことがあったりします．その場合，以下の6種類のコマンドを用いて空白を微調整します．

\qquad % \quad の2倍（数式外でも利用可能）
\quad  % 全角とほぼ同じ幅（数式外でも利用可能）
\,     % \quad の 3/18 （数式外でも利用可能）
\>     % \quad の 4/18
\;     % \quad の 5/18
\!     % \quad の -3/18（負の空白）

また，\mathstrut と呼ばれる幅0の「支柱」や，中身の高さと深さを0にする \smash{ … } なども，記号位置の微調整には効果があります．
以下がこうした空白や記号位置の微調整の例です．

例1: $\int_0^\infty e^{-x^2}\,dx = \sqrt{\pi}/2$
例2: $A^2\!/2=\sqrt{5}\,y$
例3: $R_i{}^j{}_{kl}=\int_0^1\!\int_i^j f_k(x,ly)\,dy\,dx$
例4: $\Gamma_2\Delta^2\neq\Gamma\!_2\Delta\!^2$
\[
 R_n = R_{n-1}+R_{n-2}+R_{n-3},\qquad n\ge 3.
\]
例5: $\hat{h}\hat{x}\neq \hat{\mathstrut h}\hat{\mathstrut x}$
例6: $\sqrt{h}+\sqrt{x}+\sqrt{g}\neq
      \sqrt{\mathstrut h}+\sqrt{\mathstrut x}+\sqrt{\mathstrut g}$
例7: $\underline{x}\underline{y}$? $\underline{\smash{x}}\underline{\smash{y}}$?
\[
 \left(\vphantom{\int}a\right),\qquad \left(\int a\right)
\]

空白の微調整

数式記号の種別

数式中の記号は次の 8 種類にわかれており，どの種類の記号とどの種類の記号が続いたかによって，間の空白量が変わるようになっています．

  • 普通の文字（\mathord{ … }）
  • 単項演算子（\mathop{ … }），二項演算子（\mathbin{ … }）
  • 関係演算子（\mathrel{ … }）
  • 開き括弧（\mathopen{ … }）と閉じ括弧（\mathclose{ … }）
  • 句読点（\mathpunct{ … }）
  • 部分数式（{ … } で囲まれた部分など）

そのため，LaTeX で数式を記述する際には記号が上の種類の中のどれにあるのか考えることが大切です．典型的な間違いとして，以下のようなものがあります：

$<a>$, $f:X\rightarrow Y$, $\{a|a>4\}$, $A=]0,1]$ % ←半開区間

これらは以下のように入力されるのが正解です：

$\mathopen{<}a\mathclose{>}$, $f\colon X\rightarrow Y$,
$\{\,a\mid a>4\,\}$, $A=\mathopen{]}0,1]$

数式記号の種別

  • 山形括弧は，普通は
    $\langle a\rangle$, $\left< a\right>$

    を用います（どちらも同じ括弧になります）．
    「どうしても不等号と同じ字形で出したい！」というときのみ，上の$\mathopen{<}a\mathclose{>}$ を用いて下さい．

  • \left, \right によって出力した括弧は常に開き括弧・閉じ括弧のように扱われます．そのため，上に述べた半開区間の例は
    $A=\left]0,1\right]$

    と入力しても構いません．

  • |, \| は単独では「普通の文字」扱いです．そのため，例えば
    $|-a| = |a|$

    と打ったときには空白が正しくなくなります（前節 hwb27.7 数式の書き方(1) にも例を載せました）．

    $|{-a}| = |a|$, $\mathopen{|}-a\mathclose{|}$

    のように打ってもいいですが，すぐ後で述べる amsmath パッケージで定義されている \lvert, \rvert, \lVert, \rVert を使って，

    $\lvert -a\rvert = \lvert a\rvert$

    のように打つと安全です．

 amsmath パッケージ

数式を書く場合には， 米国数学会の開発した amsmath パッケージ・amssymb パッケージを利用するのが便利です．amsmath パッケージでは，行列・複数の数式を並べる環境などが整備されており，読み込んでおくのを習慣とすると便利でしょう．
amssymb パッケージは，標準の LaTeX では提供されない数々の数式記号を提供します（「∴」「∵」もそこには含まれます）が，詳細については専門書に譲ります．

行列

行列を書くには，array 環境と \left, \right を用いるという手もありますが，pmatrix 環境などを用いるのが楽です．

\texttt{pmatrix}環境は行列を組むのに使います．
\[
J_n =
\begin{pmatrix}
  j_1&1\\
     &j_2 & 1\\
     &    &\ddots & \ddots\\
     &    &       & j_n & 1
\end{pmatrix}
\]

行列の例
類似の環境として，bmatrix, Bmatrix, vmatrix, Vmatrix 環境があります．これらでは，左右の括弧 ( ) がそれぞれ [ ], { }, | |, || || になっています．例えば行列式を書くような際には，vmatrix 環境を使うことになるでしょう．

\text{ … } コマンドと equation 環境

数式の途中に地の文を書くためには，\text{ … } を用います．添字中では自動的に文字のサイズが小さくなります．hwb27.7 数式の書き方(1) で述べたように，数式中に日本語で説明を加えたいような場合はこの \text を用いて下さい．
話は変わりますが，別行立て数式に数式番号を振るには equation 環境を用います．数式番号は自動で割り振られ，あとから再利用することができます（hwb27.9 相互参照と文献 を参照）．
以下に，\text と equation 環境の例を示します．

\[
 A_{\text{min}} = \text{some constant} = \text{ある定数}
\]
\texttt{equation}環境を使うと数式に番号をつけることができます．
\begin{equation}
E=mc^2
\end{equation}
\texttt{amsmath}パッケージ下の\texttt{equation}環境では，
数式が長い場合は番号がかぶらないように移動します：
\begin{equation}
\zeta(3) := \sum_{n=1}^{\infty} \frac{1}{n^3}
  = \prod_{p\colon \text{prime}} \frac{1}{1-p^{-3}}
  = 1.2020569\cdots
\end{equation}

\text, equation 環境の例
数式番号は，\tag{ … } コマンドを使って自分で指定することもできます．

multline, align, gather 環境

この 3 つの環境は，複数行の数式を組む時に使います．

  • \\ で数式の行を区切ります（最後の行には不要）．ソース中の見た目の改行では区切られません．
  • どの3つの環境も，最後に * をつける（align* のように）と，どの行にも数式番号がつかなくなります．
  • また，\notag と書くことでその行の数式番号をつけないようにできます．

まず multline 環境は，複数行にわたる長い 1 つの数式を組む場合に使います．先頭行は左寄せ，最後の行は右寄せ，それ以外は中央揃えとなります．
次に align 環境は，複数の数式を揃えて組むのに使います．奇数番目の & のところで横方向の位置が揃います．
最後に，gather 環境は複数の数式を単に並べるのに使います．equation 環境や \[ … \] を複数個並べるより，1つの gather 環境の中にまとめてしまった方が見栄えがよくなります．
以下に，これら 3 環境の例を示します．\notag, \tag, * つきの環境の例にもなっています．

\texttt{multline}環境は長い1数式を組むのに使います．
\begin{multline}
A+B+C+D+E+F+G+H+I\\
{}+J+K+L+M+N+O\\
{}+P+Q+R+S+T+U\\
{}+V+X+Y+Z
\end{multline}
\texttt{align}環境では数式を揃えることができます．
\begin{align}
0+a    &=a       & 1a   &=a    \\
(-a)+a &=0                      \notag\\
a+b    &=b+a     & ab   &=ba    \tag{$*$}\\
(a+b)+c&=a+(b+c) & (ab)c&=a(bc) \\
(a+b)c &=ac+bc
\end{align}
\texttt{gather}環境は複数の数式を横に揃えずに組みます．
\begin{gather*}
\sin 2\theta = 2\sin\theta\cos\theta, \\
\cos 2\theta = 2\cos^2\theta-1 = 1-2\sin^2\theta, \\
\tan 2\theta = \frac{2\tan \theta}{1-2\tan^2\theta}.
\end{gather*}

multline 環境等の例

split, aligned, gathered, cases 環境

multline, align, gather 環境はそれだけで別行立て数式になりました．一方，ここで紹介する4つの環境は，別行立て数式（つまり \[ … \] や equation 環境）の中で使うものです．
最初の3つは，複数行の式をまとめて1つの式のように扱う環境です．split と aligned は似ていますが，後者の方が複数の式全体にわたる括弧などをつけられたりと，より柔軟です．

\texttt{split}環境は，複数行にわたる1つの数式を組むのに使います．
\texttt{multline}環境と異なる所は，\verb|&|により位置ぞろえが可能な点です．
\begin{equation}
\begin{split}
V&=\frac{1}{3}\cdot 3\sqrt{3}\cdot \frac{\sqrt{3}\cdot 6^2}{4}\\
&=18\sqrt{2}.
\end{split}
\end{equation}
数式番号の位置に注目して下さい．
以下は\texttt{aligned}, \texttt{gathered}環境の使用例：
\[
 \left.
 \begin{aligned}
  \bm{\nabla}\cdot \bm{D}& =\rho,\\
  \bm{\nabla}\cdot \bm{B}&= 0, \\
  \bm{\nabla}\times \bm{E}&= -\frac{\partial\bm{B}}{\partial t},\\
  \bm{\nabla}\times \bm{H}& = \bm{j} + \frac{\partial\bm{D}}{\partial t}
 \end{aligned}
 \right\}
 \qquad \text{Maxwell方程式}
\]
例えば
$\begin{gathered}
a=b\\ c+d=e
\end{gathered}$
のように文中に複数行の数式を割り込ませることも可能ですが，
見栄えがあまり良くないです．

split 環境など
とくに，「場合分け」は数式で頻出するものです．amsmath パッケージでは，そのために専用の cases 環境が用意されています．

\texttt{cases}環境は，場合分けの記述に使います．
\begin{equation}
|a| =
\begin{cases}
a  & \text{if $a>0$,}\\
-a & \text{if $a<0$.}
\end{cases}
\end{equation}

cases 環境