29.3 文字式の計算など

前の節では Mathematica で数の計算をしましたが，もちろん文字を使うこともできますし，また関数を自由に定義することもできます．この節では，もう少し数学らしい Mathematica の使い方を説明します．

文字式の計算

文字式を扱うのは難しくありません．数と同じように，式の中に文字を打つだけで使えます．例えば x*x と入力してを押すと，x の 2 乗が帰ってきます．

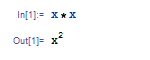
*の代わりにスペースを打って x x と入力しても，同じ結果を返してくれます．しかしスペースを打たずに xx と入力すると，Mathematica は xx という名前の変数として処理します．

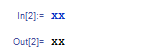
Mathematica に文字式の変形をさせるときは，明示的に命令をする必要があります．まず式の展開をするには Expand 関数を使います．たとえば Expand[(x+y)³] と入力してを押すと，x³+3x²y+3x y²+y³ になります．

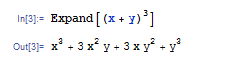
逆に因数分解をするには Factor 関数を使います．たとえば t³-1 を因数分解するには Factor[t³-1] と入力してを押します．

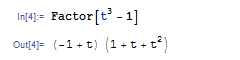
次に有理式を扱ってみましょう．有理式の通分は Together コマンドを使います．たとえば次の式を通分してみます．式の中の i は虚数単位の i で，普通のアルファベット i とは違う特別な文字で表されます．このiは文字パレットで i ボタンを押して入力するか，あるいは大文字で I と入力してください．

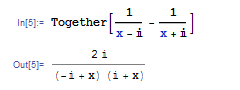
これの分母を展開させるには ExpandDenominator 関数を使います．

また分母が因数分解できる場合， Apart 関数で部分分数分解ができます．

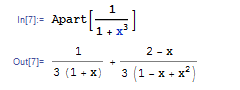
Mathematica の式の扱い方は，時と場合によって異なります．必要に応じて上記の関数を利用して，望ましい形を得るようにしましょう．

Σ と Π

Mathematica では Σ や Π を使うことができます．ためしに，基本数学アシスタントのパレット内にある Σ ボタンを押してみてください．するとノートブック上に Σ 記号が現れます．

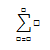
ここに普通の数式と同じように入力すれば Σ の計算ができます．たとえば k を 1 から n まで動かして k² の和を取ると，有名な公式がでてきます．

また和は有限である必要はありません．基本数学アシスタントのパレットにある ∞ ボタンを押せば ∞ 記号が入力できます．これを使えば無限和の計算もできます．たとえば n を 1 から ∞ まで動かして (-1)^n-1/ n の和を取ると Log[2] になります．

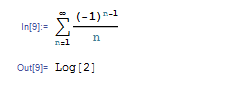
Σ 記号は項の和を計算しますが，Π 記号を使うと項の積を計算します．たとえば (1- 1/n²) を2以上の自然数 n にわたってかけあわせると 1/2 になります．

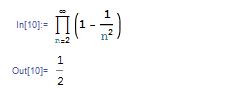
変数の定義

普通に数学をするのと同じように，Mathematica でも式などを文字で置くことができます．たとえば A=x+y と入力してを押すと，A に x+y が代入されます．

A とだけ入力してを押すと，確かに上で打った通り x+y が表示されます．

Expand[A³] と入力すると，(x+y)³ を展開した結果が出ます．

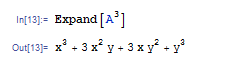
ノートブック内で定義した変数は Mathematica が終了するまで有効です．異なるノートブックであっても変数は共通で使えるようになっているので，場合によっては別のノートブックで行った計算の影響を受けてしまうことがあります．それを防ぐためには変数の消去をします．たとえば Clear[A] とすると，上で定義した A の内容が消去されます． A をクリアした後に A と打ち込んでと打っても，何も出てきません．

もちろん文字でおけるのは式だけではありません．数や行列なども文字でおくことができます．

関数の定義

関数の定義は F[x_] = … という形で書きます．たとえば F[x_]=x²+x+41 と入力してを押すと，右辺の式で F[x] が定義されます．

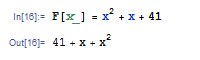
定義した関数は普通の関数と同様に使うことができます．たとえば F[3] と入力すると F の 3 における値が計算できます．

関数の定義は再帰的に行うこともできます．たとえば 100 以下の整数 n に対して G[G[n+11]] を返し，100 より大きい整数 n に対して n-10 を返す関数を McCarthy の 91 関数といいます．

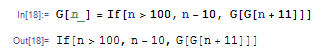
この関数は 101 以下の整数に対して必ず 91 を返します．

なお関数の定義には即時割り当て，遅延割り当てと呼ばれる二つの方法があります．上で用いた定義は即時割り当てと呼ばれるものです．上のように数学的な関数を定義するだけなら即時割り当てを使えば大丈夫です．遅延割り当てについては，後で必要になったときに説明します．