29.7 パラメータの変化に関する挙動の追跡

数学などでは，よく式やグラフにパラメータが入り「パラメータの値によってどう状況が変わるか」を追跡したいことがあります．Mathematica には Manipulate という関数があり，これを使うと自由自在にパラメータを動かせます．非常に便利な機能ですので，ぜひ使ってみてください．

問題例

今回は y² = x³ + ax という方程式で決まる曲線の様子が，パラメータ a にどう依存しているかを調べましょう．この曲線は楕円曲線と呼ばれるものの一種です．方程式中で y に依存する項が y² しかないため，この曲線は常に x 軸に対して対称な形となります．しかし a の値に応じて，見た目に大きな変化があります．まずは陰関数のグラフを描くための ContourPlot 関数（29.6 グラフの描き方）を使って，グラフの様子を把握しましょう．
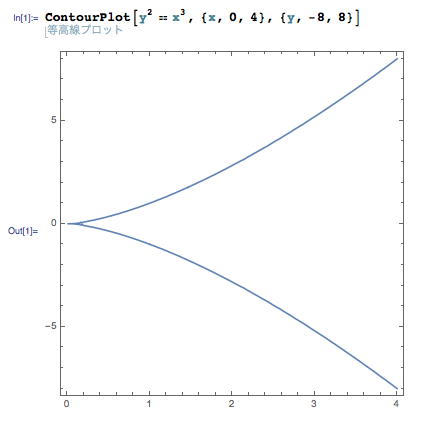
a = 0 の場合， x³ が 0 以上になるには x が 0 以上でないといけないので，y² = x³ のグラフが現れるのは座標軸の右側です．そしてこの式を x について解いた式 x = y^2/3 は微分係数が x = 0 で発散するので，原点では尖った形になります．

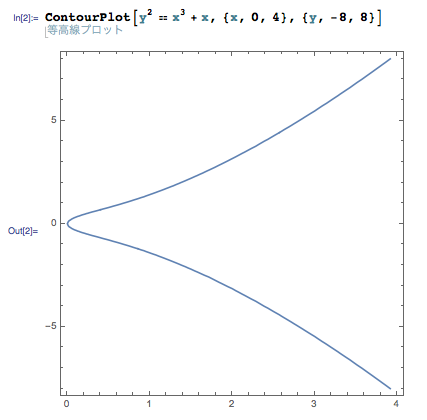
a = 1 の場合， y² = x (x² + 1) の右辺が正になるには x が 0 以上でないといけないので，やはりグラフが現れるのは座標軸の右側です．ただし a = 0 のときとは違い，原点でこの曲線は滑らかになります．このことは関数 F(x, y) = y² – (x³ + ax) の Jacobi 行列が原点でフルランクなことから，陰関数定理を使って分かります．

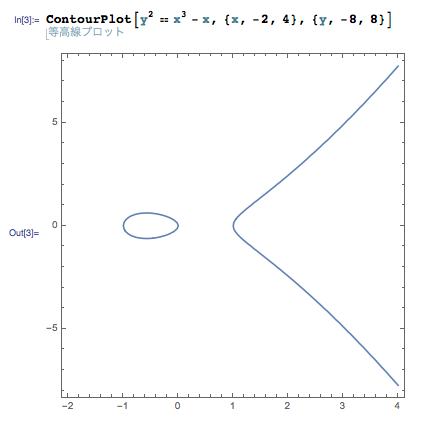
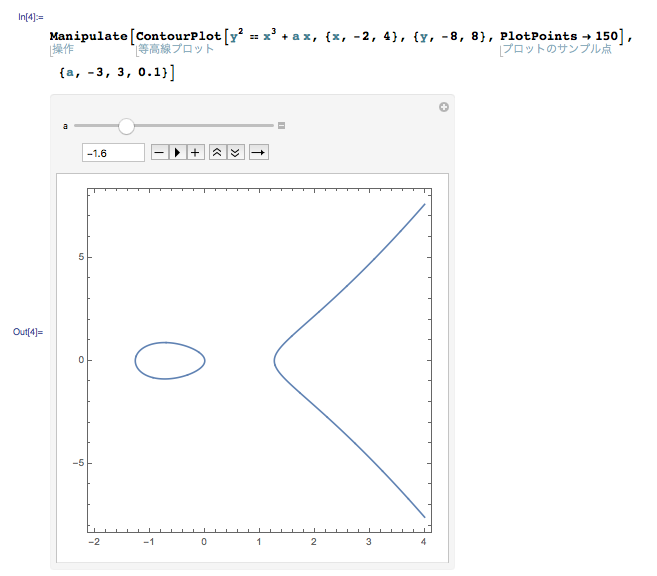
そして a = -1 の場合， y² = x³ – x の右辺が x (x + 1)(x – 1) と因数分解できるため，右辺が 0 以上になる x の値が「-1 以上 0 以下」と「1 以上」の 2 つに分裂します．そのため，グラフは 2 つの連結な成分に分かれます．この場合も a = 1 と同様，原点ではグラフは滑らかです．また Jacobi 行列の計算によって，x = 0, -1 でも滑らかなことが分かります．

では a を動かしたとき，これら 3 つのグラフはどのように繋がるのでしょうか？それを実際に，Manipulate 関数で見てみましょう．

Manipulate 関数の使い方

Mathematica に Manipulate[ ContourPlot[ y² == x³ + a x, {x, -2, 4}, {y, -8, 8}, PlotPoints->150 ], {a, -3, 3, 0.1} ] と打ち込んでみてください．次のように，スライダー付きのグラフが表示されるはずです．

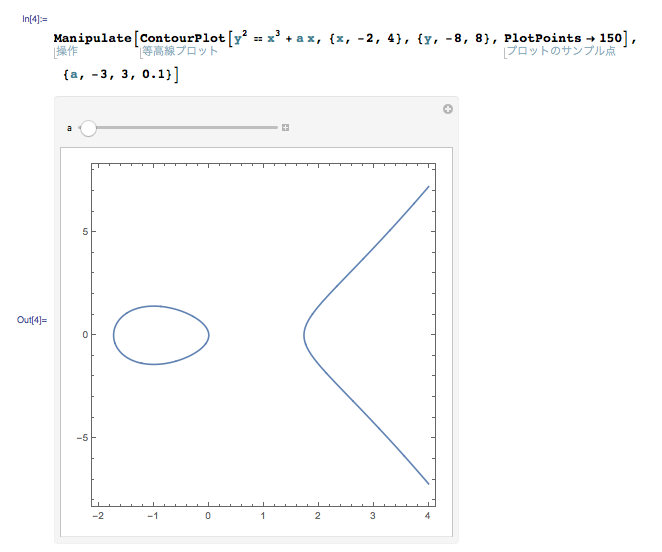
このように Manipulate 関数は「パラメータの入ったグラフや式」を最初に与えてから，{a, -3, 3, 0.1} のように「動かす変数」「動かす範囲の下限」「動かす範囲の上限」「刻み幅」を中括弧で並べたリストで指定します．なお，刻み幅は省略可能です．
そして，このグラフはスライダーを動かして変化させられます．

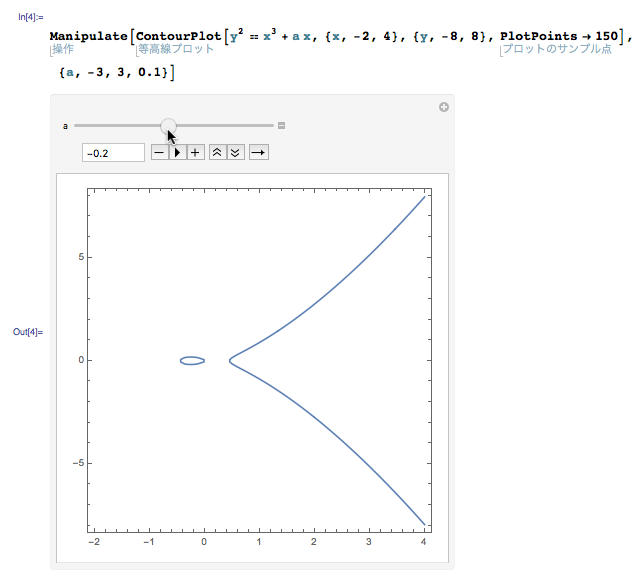
これによって，a の値が負の方向から 0 に近づく時，左の連結成分がどんどん潰れてくることが分かります．また左右の連結成分がくっつくのが a = 0 のときで，その瞬間に原点が特異点となっていることが分かります．ぜひ実際に動かしてみてください．
また，スライダーの横にある + ボタンを押すと，下に細かいメニューが展開されます．

このメニューを使うと，

直接パラメータの数値を指定する
予め与えた刻み幅で 1 段階ずつパラメータの値を変化させる
アニメーションを実行する

といった操作ができます．