![[HWB]](/image/hwb3.png "[HWB]"){kind=small}
Mathematica では行列の計算もすることができます．この節では，行列に関連する様々な計算のやり方を紹介します．
行列の入力
まず行列を入力するには，メニューバーをとたどります．
すると行列を作成するためのダイアログが開きます．
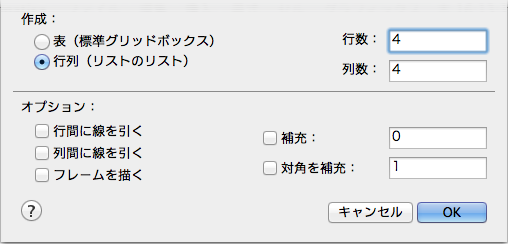
ここの行数と列数を入力して OK ボタンを押すと，行列ができます．たとえば行数と列数をそれぞれ 3 と 4 にして OK ボタンを押すと，次のようにサイズ 3×4 の行列がノートブックに現れます．
よく使われる 2 次正方行列は，基本数学アシスタントのパレットからも入力できます．パレットの「タイプセット」のところをクリックして展開すると，いかにも行列らしいボタンがあるのが分かります．
各セルをクリックすることで数を入力できます．また，成分の入力中に 
を押すと右隣のセルに，
を押すと左隣のセルに移動することができます．
行列の計算
行列の足し算は数と全く同様にできます．たとえば次の図のように 2 つの行列の間に + をはさんで 
を押すと，行列を足した結果が出てきます．
計算結果の見た目が行列の格好をしていませんが，{6, 8} が 1 行目，{10, 12} が 2 行目に対応しています．このままでも読めなくはないですが，MatrixForm 関数を使うと見やすい行列の形にすることができます．
Mathematica では F[x] と x // F が同じ意味を持ちます．なので上の MatrixForm を用いた表示は，次のようにしても実現できます．
見やすいほうが嬉しいので，以下で行列の演算をするときは全て最後に // MatrixForm をつけることにします．
行列のスカラー倍は，行列の前に数を書くだけで計算できます．たとえば次の例のようにして，行列を 3 倍することができます．
行列のかけ算をするには注意が必要です．二つの行列の間に * を書くと，普通の行列の積ではなく，成分同士のかけ算になってしまいます．たとえば次の例では，2 次の単位行列をかけているにもかかわらず (1,2) 成分と (2,1) 成分が 0 へと変化しています．これで確かに，成分ごとのかけ算が行われたと分かります．
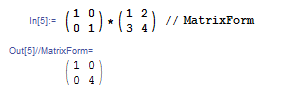
普通の行列のかけ算をするには，行列の間にドット . を打ちます．
かけ算の記号 * が成分ごとの積を意味するので，行列の巾乗も成分ごとになってしまいます．たとえば {{0, 1}, {1, 1}} を巾乗の記号で 3 乗すると，何も変わりません．
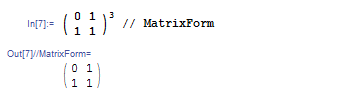
これを正しく 3 乗するには MatrixPower 関数を使います．次の図のようにすれば 3 乗が計算できます．
4 乗，5 乗なども試して，正しく計算できていることを確認してください．
正方行列が正則なときは逆行列が取れます．逆行列は Inverse 関数で計算できます．たとえば Inverse[{{1, 1}, {0, 1}}] とすると，行列 {{1, 1}, {0, 1}} の逆行列が求まります．
この結果と {{1, 1}, {0, 1}} の積を取ると，確かに単位行列になります．
転置と対角和(トレース)
行列の転置を取るには Transpose 関数を使います．たとえば Transpose[{{a}, {b}}] を入力して を押すと，縦ベクトルが横ベクトルに変わります．
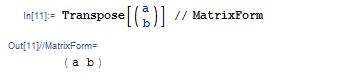
横ベクトルと縦ベクトルをかければ，普通の内積が出てきます．
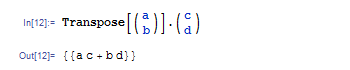
また複素共役転置は ConjugateTranspose 関数を使うと計算できます．次の例では，ベクトル{{2+3i}, {1+2i}} の Hermite 内積でのノルムを計算しています．
正方行列の対角和(トレース)を計算するには Tr 関数を使います．例えば Tr[{{a, b}, {c, d}] を計算させると，確かに a+d が出てきます．
勝手な行列 A, B に対し，AB と BA の対角和は一致します．この事実を2次正方行列の場合に確認しましょう．
また転置とトレースを組み合わせれば，行列の各成分の二乗和が求まります．
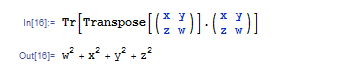
行列式の計算
正方行列の行列式を計算するには Det 関数を使います．Det[] のかっこの中に正方行列を書いて を押すと，行列式を計算してくれます．
行列の成分は数である必要はなく，文字が入っていても計算できます．たとえば次の例では Vandermonde の行列式を計算しています．
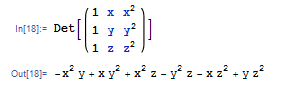
完全に展開された結果が表示されますが，上の計算に引き続き Factor[%] と打って因数分解すると差積の形になります．
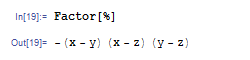
行列式を利用すれば，行列の固有多項式も計算できます．たとえば次の例では，行列 {{0, 0, 1}, {1, 0, 0}, {0, 1, 0}} の固有多項式を計算しています．名前から明らかですが，式中の IdentityMatrix 関数は単位行列を表す関数です．
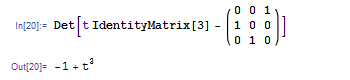
固有値，固有ベクトルの計算
上で Det 関数を用いて固有多項式を計算しましたが，固有多項式は CharacteristicPolynomial 関数でも計算できます．すぐ上の例をもう一度計算してみましょう．同じ行列を何回も使うので A とおいておきます．
CharacteristicPolynomial 関数を使うと，符号は逆になっていますが同じ多項式が出ます．2番目の引数の t は，固有多項式の変数を表します．
Eigenvalues 関数を使うと，行列の固有値一覧が表示されます．今の行列の場合，1 の 3 乗根が 3 つとも出てきます．
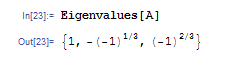
また Eigenvectors 関数を使えば，今度は各固有値ごとに固有ベクトルを得ることができます．ただし出力結果は列ベクトルになっています．
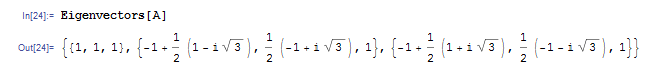
正方行列の Jordan 標準形は JordanDecomposition 関数で計算できます．JordanDecomposition 関数は 2 つの行列を返してきます．たとえば上の例では，次のような行列が得られます．
2 つ目の行列が Jordan 標準形です．1 つ目の行列は，標準形に変形する際に使う行列です．1 つ目に出てきた行列を P とおきます．
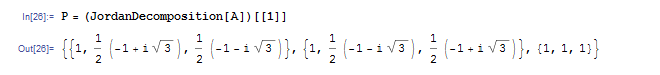
P-1AP を計算すると，えげつない行列が出てきます．
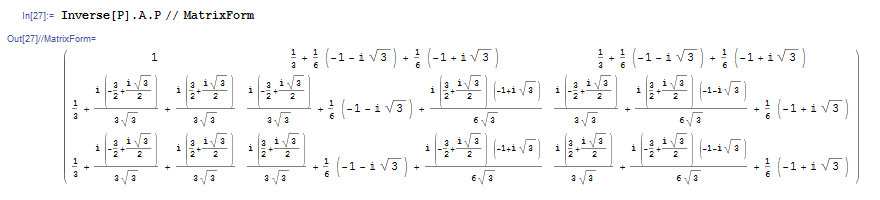
しかし Simplify をすれば見やすい形になり，先ほどの固有値の計算結果通りになることが分かります．
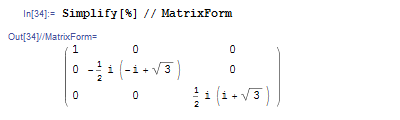
行列の指数関数
普通の指数関数 Exp[x] は次の巾級数で定義されます．
この巾級数には正方行列を代入することができます (無限和なので各成分が収束するか評価する必要がありますが，実は任意の行列に対して収束することが証明できます)．そこで，この巾級数で行列の指数関数を定義します．
Mathematica で行列の指数関数を計算するには MatrixExp 関数を使います．たとえば行列 {{0, t, 0}, {0, 0, t}, {0, 0, 0}} の指数関数を計算するには次のようにします．
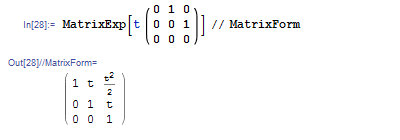
ちなみに，いま MatrixExp を計算した行列は 3 乗すると 0 になります．
よって収束の議論をするまでもなく，指数関数の定義に基づいて計算することが可能です．MatrixExp 関数で計算した結果と一致しますね．
もちろん，巾零行列でなくても指数関数は計算できます．たとえば行列 {{0, -t}, {t, 0}} の指数関数を計算すると回転行列が現れます．
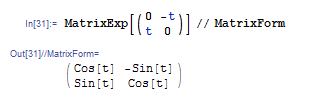
これにより，2 次元の場合に交代行列の Exp が回転行列になることが分かります．大げさに言えば，回転行列のなす Lie 群 SO(2) とその Lie 環 so(2) の対応を見ていることになります．