23.2.14 科学技術計算の簡単な例

Excel を用いると，科学技術の分野で出てくる数値計算を行うことができます．Excel では高度な計算や精密な誤差評価まではできませんが，ちょこっと実験的に計算をするだけなら簡単です．
今回は例として √2 = 1.41421356… の近似計算の実験を，Excel でやってみたいと思います．√2 は，放物線 y = x² – 2 と x 軸の交点のうち x>0 の領域にあるものです．ですから √2 の計算は「関数 f(x) = x² – 2 に対し，f(x) = 0 を満たす点 x を求める」という問題に言い換えられます．このような方程式の解を数値的に求める手法として，二分法と Newton 法というものが良く知られています．

二分法

二分法は，ある関数の値が 0 になる場所を，区間幅を半分に狭めながら探っていく手法です．

二分法の原理

関数 f(x) = x² – 2 は区間 [0, 2] で短調増加です．さらに f(0) = -2 と f(2) = 2を合わせると，区間 [0, 2] 上に f(x) = 0 となる点が唯一存在することが分かります．これを使うと「区間を左半分と右半分とに分けて，どっちに f(x) = 0 が含まれるかを調べる」という操作を十分な回数繰り返すことで，f(x) = 0 となる x の範囲を狭めていくことができます．いまの場合

1. 区間 [0, 2] の中点では f(1) = -1 < 0 なので，f(x) = 0 の解は [1, 2] 上のどこかにある
2. 区間 [1, 2] の中点では f(3/2) = 1/4 > 0 なので，f(x) = 0 の解は [1, 3/2] 上のどこかにある
3. ……

といった操作を繰り返すことになります．このステップを 1 回行うごとに解の存在し得る範囲を半分に狭められますから，n ステップ進めることで区間の幅を 2^-n にできます．

実際の計算

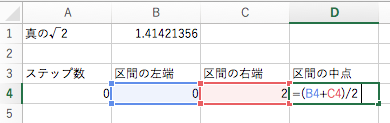
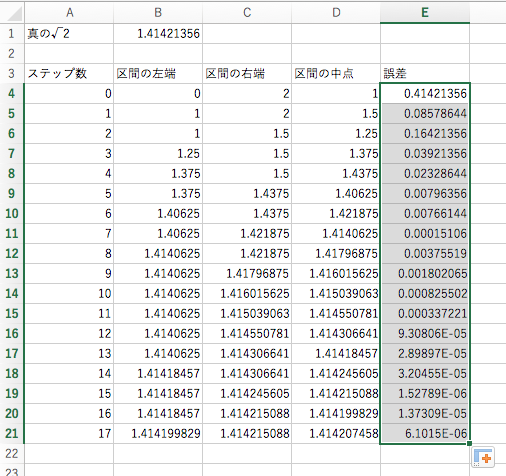
それでは実際に，二分法で √2 の計算をしてみましょう．今回は計算の技法を理解することが目的ですから，予めセル A1 に「真の √2」，セル A2 に 1.41421356 を書き込んでおきましょう．その上でセル A3, B3, C3, D3 の順にそれぞれ「ステップ数」「区間の左端」「区間の右端」「区間の中点」と書き込みます．以下，この下に計算の情報を書き込むことになります．
まずは初期値の設定です．最初のステップ数は 0 なので，セル A4 に 0 を入力します．また最初は区間を [0, 2] に取るので，区間の左端 B4 には 0, 区間の右端 C4 には 2 を設定します．そして最後に，区間の中点 D4 に式

=(B4+C4)/2

を書きます．ここまでの状況は，次の図のようになっているはずです．

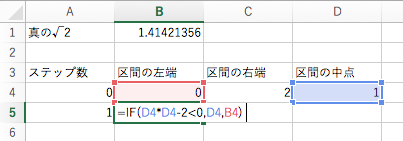
続いて，1 ステップ進めた後の計算を書きましょう．セル A5 には 1 を書き込みます．そして前のステップにおける区間の中点で x² – 2 の値を見て

• 符号が負だったら，次のステップにおける区間の左端は，前のステップにおける区間の中点へと更新する
• 符号が正だったら，次のステップにおける区間の左端は，前のステップにおける区間の左端から動かさない

というようにします．これは Excel の IF 関数を用いると

=IF(D4*D4-2<0,D4,B4)

と表せます．これをセル B5 に書き込みましょう．

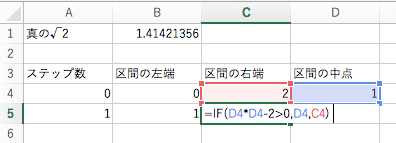
区間の右端も，同様に考えます．右端の場合は，前のステップにおける区間の中点での x² – 2 の値を見て

• 符号が正だったら，次のステップにおける区間の右端は，前のステップにおける区間の中点へと更新する
• 符号が負だったら，次のステップにおける区間の右端は，前のステップにおける区間の右端から動かさない

という操作をします．ですから Excel の式で書けば

=IF(D4*D4-2>0,D4,C4)

となります．これをセル C5 に書き込みましょう．

区間の中点 D5 の式は D4 の行番号をずらすだけなので，D4 の式をコピー & ペーストすれば埋まります．ここまでできれば，次のステップ移行もやることは全く同じです．したがって行全体を下方向にコピー & ペーストすれば，自動的に行番号が 1 つずつズレた式が入り，計算が行われます．

ちゃんと √2 の値に近づいていることを，確認してください．
計算の後は，誤差の評価をしましょう．たとえば 0 ステップ目での誤差は，D4 – $B$4 です．そこでセル E3 に「誤差」と書き，その下のセル E4 に

=ABS(D4-$B$1)

と書きます．ここで，実際に知りたいのは「誤差の大きさ」だけですから，絶対値を意味する ABS 関数を施しておきました．

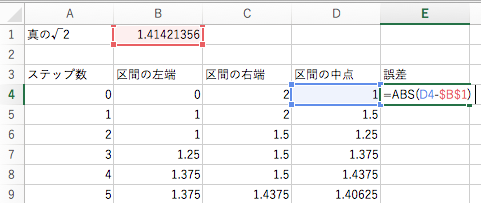
あとはオートフィルなりコピー & ペーストなりで，セル E4 の中身を下の方まで埋めましょう．そうすると，各ステップにおける誤差が数値で現れます．

ここで現れた E-05 や E-06 は指数表記の略記法で，それぞれ 10^-5, 10^-6 を表します．0.00… のように 1 の位から書き始めると値が長くなりすぎるので，このように書かれます．これで確かに，ステップを進めるごとに誤差が 0 へと近づいていることが分かりますね．

Newton 法

Newton 法は，接線を使って f(x) = 0 の解の場所を調べる方法です．

Newton 法の原理

既に述べたように，関数 f(x) = x² – 2 は区間 [0, 2] 上で 1 回だけ値が 0 になります．そして f”(x) = 2 なので，y = f(x) のグラフは下に凸です．そこで x = 2 を出発点として「接線を引き，それの x 切片を求める」という操作を繰り返すことで，f(x) = 0 となる x の値に近づくことができます．
今の場合，放物線 y = x² – 2 の x = t における接線は，微分を用いると y = 2tx – t² – 2 と求まります．したがって

1. x = 2 における接線 y = 4x – 6 の x 切片は 3/2 である
2. x = 3/2 における接線 y = 3x – 17/4 の x 切片は 17/12 である
3. ……

という操作を繰り返していくことになります．

実際の計算

この計算もやってみましょう．後で二分法と Newton 法の性能を比較したいので，二分法の計算をしたのと同じシート上で Newton 法の計算を行いましょう．
セル G3, H3 にそれぞれ「ステップ数」「値」という見出しを作ります．その後初期値として，セル G4 に 0 を，セル H4 に 2 を書き込みます．

続いて，ステップを進めるにはどうすれば良いか考えましょう．放物線 y = x² – 2 の x = t における接線は y = 2tx – t² – 2 で与えられます．そしてこの直線の x 切片は，y = 0 とおくことで x = (t² + 2) / (2t) と求まります．ですから t に対して (t² + 2) / (2t) を対応させることが，1 ステップ進める計算に相当します．これを行うため，セル G5 に 1 を入力した後，セル H5 に

=(H4*H4+2)/(2*H4)

を入力します．1 つ前のステップにおける値 H4 を，今求めた式に代入しているわけです．また掛け算と割り算の順序を明示的に指定するため，かっこを使っています．

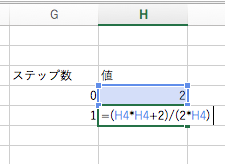
そして，G2 と H2 を合わせて下にコピー & ペーストすれば，先のステップまで計算ができます．

これが終わったら，やはり誤差の評価を行います．二分法のときと同様，セル I4 に

=ABS(H4-$B$1)

を書き込みましょう．

これを下の方までコピー & ペーストすると，各ステップにおける誤差が見えます．

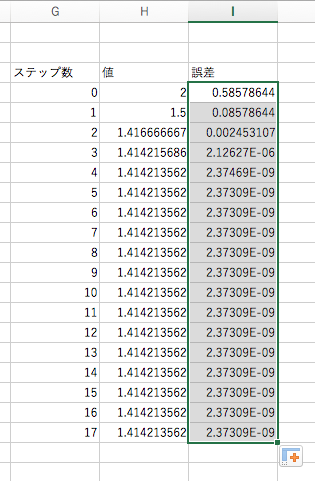
4 ステップ目から先で値の更新がないことが分かります．これは Newton 方の精度が良いため，少ないステップ数で Excel の精度の限界に達したことを表しています．

誤差評価

最後に，誤差のプロットをしてみましょう．既に Newton 法の方が二分法より高精度だという雰囲気が漂ってはいますが，グラフにすることで，その事実が一段と明らかになります．
まず，二分法と Newton 法それぞれの誤差の一覧を選択して，折れ線グラフを描いてみましょう．

確かに二分法より，Newton 法の方が性能が良さそうです．

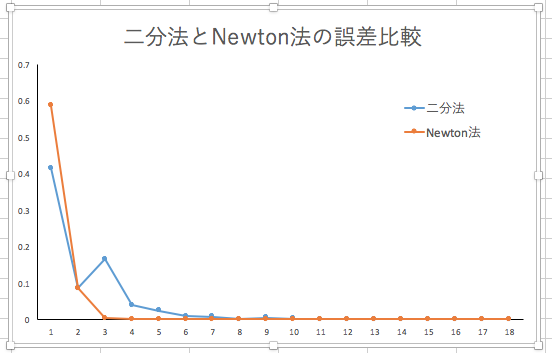
この事実をさらに細かく確認するには，対数プロットを使います．縦軸を対数スケールに取り換えましょう．そうすると，誤差が大体直線的に変化していくことが分かります．

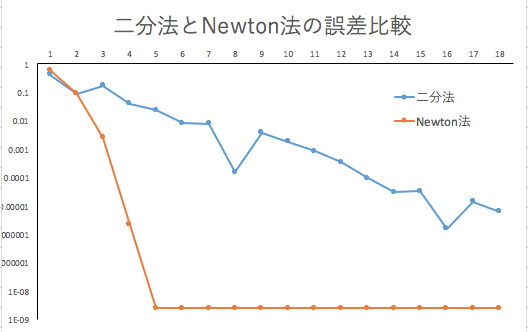
実際に数学的に評価を行うと，Newton 法の方が二分法よりも早く真の値に収束することが証明できます．そのことを反映して，二分法より Newton 法の方が急勾配になっているのです．