18.7.2 圧縮アルゴリズム

圧縮アルゴリズムの一例として Huffman 符号化を説明します．いわゆる「ファイルを圧縮」する場合にこの方法を単独で用いることはほとんどないですが，zip 形式を始めとする多くのアルゴリズムで部分的に Huffman 符号化が使われています．

Huffman 符号化

Huffman 符号化は「出現頻度の高い文字には短い符号を，出現頻度の低い文字には長い符号を割り当てる」というアイデアで全体を短く符号化する方法です．
この符号化では Huffman 木という木を作ることが鍵になります．まずは具体例で Huffman 符号化の方法を説明します．A, B, C, D, E という 5 つのアルファベットからなる文字列 “AEEADACDEBCDAAE” を符号化してみましょう．

各文字の出現頻度を数える．今の場合 A が 5 回，B が 1 回，C が 2 回，D が 3 回，E が 4 回です．
出現頻度が低い順に B, C を取り出し，それらを子とする木を描き，2 つの辺に 0, 1 を割り当てる．木の上側には，B, C の出現頻度を合算した数を書く．以下，BC はひとまとめにして考える．
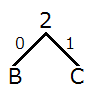
出現頻度が低い順に BC, D を取り出し，BC の木と D とを子とする木を描き，2 つの辺に 0, 1 を割り当てる．木の上側には，B, C, Dの出現頻度を合算した数を書く．以下，BCD はひとまとめにして考える．
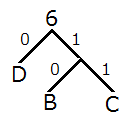
出現頻度が低い順に A, E を取り出し，A と E を子とする木を描き，2 つの辺に 0, 1 を割り当てる．木の上側には，2 つの文字の出現頻度を合算した数を書く．以下，AE はひとまとめにして考える．
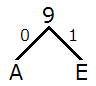
出現頻度が低い順に AE, BCD を取り出し，これらを子とする木を描き，2 つの辺に 0, 1 を割り当てる．
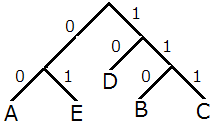
上流から各文字まで木の辺をたどり，その途中の辺上に書かれた 0, 1を並べたものを符号化とする．今の場合 A, B, C, D, E の順に 00, 110, 111, 10, 01 です．
各アルファベットを上で定めた符号で置き換える．今の “AEEADACDEBCDAAE” の場合，Huffman 符号化したものは “000101001000111100111011110000001” という 33 ビットでの 0, 1 の列で表されます．

これはちゃんとした符号化になっています．実際，符号化した後の文字列を頭から読んで

0 が出たら次の文字を読み 00 なら A, 01 なら E に直す
1 が出たら次の文字を読み 10 なら D に直す．もし 1 の次に 1 が続いたらその次も読み，110 なら B, 111 なら C に直す

というルールでアルファベットに直せば，元の文字列が復元できますね．そして単純に 0, 1 の列で A, B, C, D, E を符号化すると各文字に 3 ビットの割り当てが必要なので，元の文字列を符号化するのに 45 ビットが必要になります．これと Huffman 符号化の結果を見比べると，確かにビット数が節約できていると分かります．ただし Huffman 符号化では圧縮する対象を見て符号化の仕方を決めるので，圧縮するものが違えば符号化方法も違ってしまいます．そこで Huffman 符号化によるファイルの圧縮では，圧縮した後のファイルの先頭に符号化の方法を付け加えるようにします．
今の例を見れば，一般の場合も容易に想像が付くはずです．グラフ理論における「木」という言葉を使えば，次のように書けます．

各文字ごとに，その文字だけからなる木を作り，文字の出現頻度でラベルをする．
最もラベルの小さい 2 つの木を子とする木を作り，元々の 2 つの木は除去する．新しく出来た木のラベルは，元になった 2 つの木のラベルの和とする．また，新しく作った辺を 0 と 1 でラベルとする．この操作をできなくなるまで繰り返す．
根ノードから葉ノードまでを読んでできる 0, 1 の列を符号化とする．

Huffman 符号化は，常に可能な最短の符号化を与えることが理論的に証明できます．興味のある人は 18.9 参考文献に挙げた文献などを参照してください．