18.6.2 デジタル・アナログの変換と音声の符号化

この節では音声のデータをどのように符号化するか，またアナログ情報をデジタル情報へと変換する方法について説明します．

PCM

音は空気 (の密度) の振動です．これをデータとして記録するにはどうすれば良いでしょうか？
今はほとんど見かけなくなりましたが，1980年頃までは「レコード」と呼ばれるものが良く使われていました．レコードは大きな円板です．そして音の波形の変化を物理的な溝としてレコードに記録することで，音を記録していたのです．逆に音声を再生するときは，回転するレコードの上に針を落とし，針の位置変化を読み取っていました．
ところがコンピュータは，デジタルな情報しか処理できません．ですからコンピュータで音のデータを記録するには，何とかして振動の波形をデジタル符号化しなければいけません．そこで使われるのが PCM（パルス符号変調）方式と呼ばれるものです．パルス符号変調でデジタル符号化をするイメージは，次のような図で表せます．

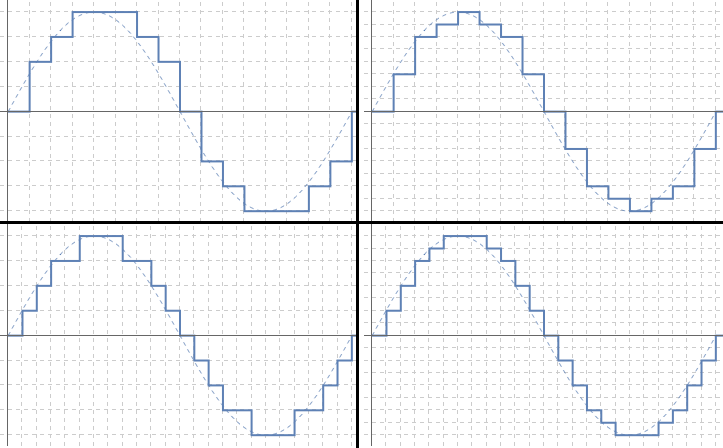
縦軸と横軸をいくつかに刻み，波をギザギザの階段で近似することがポイントです．これによって波の「振幅」という量が「刻み幅の何倍」という数値で表され，また時刻も「単位時刻いくつ分」という数値で表されます．この数値のペアを連続で記録することで，波を再現するのです．
この方法では波を近似的にしか再現できないとはいえ，コンピュータの処理速度は極めて速いですから，振幅を記録する間隔は極めて細かくできます．また振幅の刻み幅も，実際には何万段階という細かさに設定できます．このようにして「アナログデータを記録できなくても，十分細かい間隔でのデータを記録しておけば，アナログデータをある程度復号できるだろう」という方針で波形を記録するのが，PCM 方式です．

標本化と量子化

PCM 方式では，音声を録音するのにサンプリングレートおよびビット数という値を設定します．これらの値が何を意味するのか，また実際の音質にどのように反映されるのかを確かめていきましょう．
PCM 方式を使うには，上で挙げた図のように，横軸（時刻）と縦軸（振幅）の両方を等間隔に刻まないといけません．したがって PCM 方式による音声のデジタル符号化を行うには，2 つ決めなければいけないことがあります．

• どの程度細かい時間間隔で振幅を記録するか
• 振幅をどれくらい細かい刻み幅で記録するか

これらを決めると，各時刻毎の音の強さが「刻み幅の何倍か」という数値データにデジタル符号化されます．そして，この数値データを並べることで，音声全体のデジタル符号化ができます．
この際

• 時間間隔を設定して，一定時間毎に振幅のデータを記録することを標本化（サンプリング）
• 振幅の刻み幅を設定して，振幅の強さを「刻み幅の何倍」という形で段階的に表すことを量子化

といいます．また

• 1 秒間あたりの標本化の回数をサンプリングレート
• 振幅の刻み幅を表現するのに用いるビット数をビット数

といいます．たとえばサンプリングレートが 44,100Hz (= 44.1kHz) の場合，1 秒間に 44,100 回の割合で振幅を記録します．またビット数が 16 の場合，振幅の記録に 16 ビットの情報を使えるので，2¹⁶ = 65536 段階の細かさで振幅を記録できることになります．こちらの表現は市販の音楽 CD 等でも使われることがあるので，なじみがあるのではないでしょうか？
さて PCM で符号化された音声の質はサンプリングレートとビット数の両方に左右されます．標本化の回数を増やしたり振幅の記録を細かくすれば音質が良くなるのは，直感的には明らかでしょう．ですからサンプリングレートやビット数の数値が大きいほど，音質は良くなります．実際にそれを，サンプルファイルで確かめてみます．下の 6 つの音声ファイルの中から，いくつか聴き比べてみてください．

一番上の 44100Hz_16bit.wav は，サンプリングレート 44100Hz, 16bit 量子化による録音で作りました．またサンプリングされたデータの一部を捨てれば，サンプリングレートを引き下げることができます．残りのファイルは 44100Hz_16bit.wav を加工してサンプリングレートを引き下げたものです．

44100Hz_16bit.wav

32000Hz_16bit.wav

22050Hz_16bit.wav

16000Hz_16bit.wav

11025Hz_16bit.wav

08000Hz_16bit.wav

おそらく 44100Hz と 32000 Hz の間では，そこまで差を感じないのではないでしょうか？一方で 11025Hz や 8000Hz までサンプリングレートが下がると，音の劣化をはっきりと認識できるはずです．

標本化の詳細

さて，標本化の細かさが音質に影響を与えることは分かりましたが，具体的にはどの程度の影響を及ぼすのでしょうか？これを調べてみましょう．

波形の周期 vs 標本化の間隔

まず，波形データを記録するのに必要な標本化の間隔は，記録したい波形データの周期によって決まるという事実を確認しましょう．
たとえば，一番単純な波形データであるサインカーブ y = sin 2πt の標本化をしてみます．

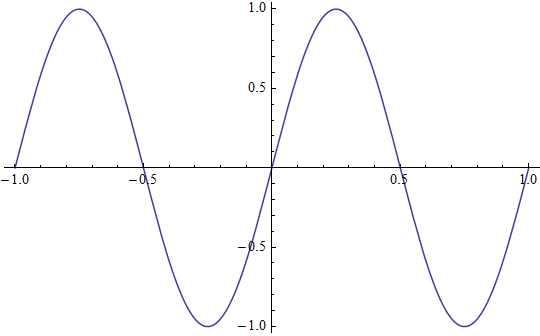
この関数の周期は 1 です．サンプリング間隔を 1/4, 1/8, 1/16, 1/32 と順次変えて標本化してみるとどうなるでしょうか？並べてみましょう．

1/4 で標本化した絵だけを見ていても，元の波形を推測するのは難しいでしょう．一方 1/16 くらいの間隔で標本化したデータを見れば，かなり正確に元の波形を推測することができるはずです．1/32 まで細かくすれば，ほとんど元の波形が見えています．周期に対して十分細かいサンプリングをすれば，元の波形が再現できそうです．
またどんなにサンプリング間隔が細かくても，周期がそれよりも大幅に小さければ無意味です．たとえば上で見たように 1/32 という標本化間隔は y = sin 2πt の標本化には十分です．しかしこの波形に 0.04 sin 128πt という細かく微小な揺らぎを加え， y = sin 2πt + 0.04 sin 128πt にしてみるとどうなるでしょうか？

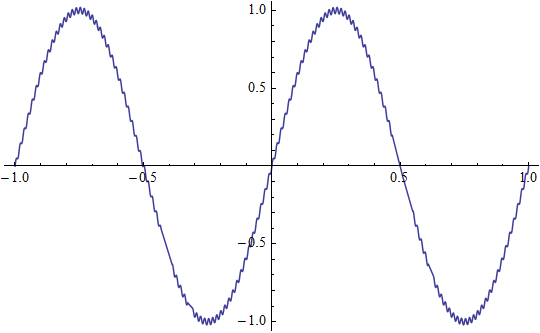
これを 1/32 の間隔でサンプリングすると，実は揺らぎが加わる前と全く同じグラフが出てきてしまうのです．

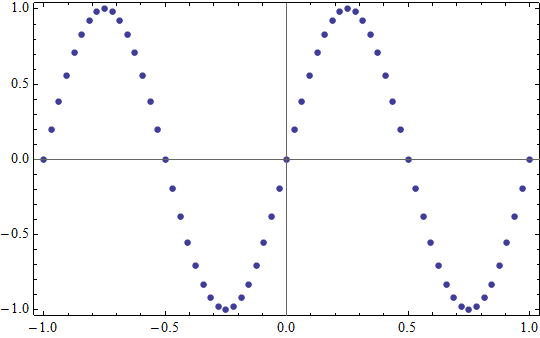
この原因は，t が 1/32 の倍数のときに sin 128πt が常に 0 になってしまうことです．sin 128πt の波形に対して 1/32 という標本化間隔が小さすぎるため，sin 128πt の値の情報が抜け落ちてしまうのです．このことからも，重要なのは「波形の周期に比較して標本化の間隔がどれくらい短いか」であることが分かります．

Fourier 変換

標本化の話をするにあたり，もう一つ知っておくべきことは Fourier 変換と呼ばれる操作です．
録音された音声などを扱う場合，サインカーブのような綺麗な周期関数が現れることはまずありません．周期的ではあっても，非常に複雑な波形が現れます．

ところが Fourier 変換と呼ばれる操作をすると，波形をサインカーブの足し算に分解できます．その情報基づいてサインカーブを足すと，元の波形にそこそこ近いグラフが得られます．
このように，一般の波形も色々な周期の波の重ね合わせで表されるのです．ですから

• どの程度の周波数までの情報を拾うかを決め
• 拾うと決めた周波数の上限に対して，十分な標本化間隔を決める

という順番で標本化間隔を決めれば，元の波形がそれなりの精度で再現できます．

標本化定理

そして，周波数が与えられたときに「どの程度の細かい標本化が必要か」を教えてくれるのが標本化定理 (sampling theorem) と呼ばれるものです．
標本化定理は「ある周波数の波形を正確に記録するには，その 2 倍の周波数以上で標本化をすればよい」ことを主張する定理です．「なぜ 2 倍か」については細かい計算が必要ですが，感覚的には理解できるのではないでしょうか？たとえば先ほどの y = sin 2πt を間隔 1/4 で標本化したデータを見てみましょう．

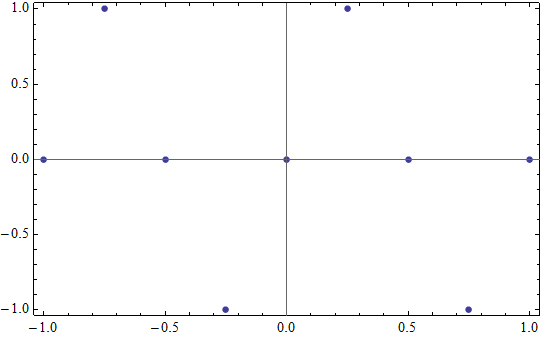
答えを隠されて「元の波を推測せよ」と言われたら，少々厳しいと思います．ですが「元のグラフは，周期 1 の関数である」というヒントがついたら，ほぼ確実に y = sin 2πt と推測できるのではないでしょうか？
また実際に標本化定理を使う場合，標本化する周期から「何 Hz の波形までのデータを取れるか」を考えることも多いです．標本化する周期が T₀ のとき，データの損失なしに標本化できる限界の周波数 1/T₀ は Nyquist 周波数と呼ばれています．

音声の標本化

以上の一般論を，音声に限定して適用してみましょう．
人間に聞こえる音には上限があり，それは大体 20000Hz = 20kHz と言われています．そして標本化定理によれば，サンプリングレートを 40kHz にすれば 20kHz 以下の音を損失無しに記録できます．よって事実上は，40kHz 程度のサンプリングをすれば人間が得られる情報の損失はないと言えます．そのため音楽 CD などでは，通常 44.1kHz でサンプリングが行われています．また，特に音質を重視する場合は，サンプリングレートをさらに引き上げることもあるようです．

(非可逆) 圧縮

PCM で符号化された音声のデータは非常に大きくなります．例えば音楽 CD で用いられる 44.1kHz サンプリングの場合，80 分の音声で 700MB のデータ量になってしまいます．そこで目的に応じて圧縮をかけ，データ量を減らすということが行われます．データ圧縮の形式や圧縮されたデータを利用するのに必要なプログラムをコーデックと言います．
非可逆圧縮の際に主に削られるのは高周波数のデータです．人間に聞こえる音はおよそ 20kHz までですが，実際は 20kHz の音を聞けることも希で，高周波数の音を落としてもそんなに聞こえ具合は変わりません．そこで人間の耳がそんなに感じない程度にデータを落とすことが行われます．また，ある音が大きい音量で聞こえるときは他の音はさほど感じられません．こういう心理的な効果を利用して，あんまり人間が感じないであろうデータも削られます．さらにデータを削った後でハフマン符号化などによる圧縮をすることで，元の PCM 音声に比べて大分データを減らすことができます．
このような非可逆圧縮を行うファイル形式としては，たとえば MP3 (Mpeg-1 Audio Layer 3), WMA (Windows Media Audio), AAC (Advanced Audio Coding) などがあります．いずれの形式も音質をさほど損なうことなくデータ量を減らしているので，インターネット上での音楽のやりとりに広く用いられています．
たとえば 44100Hz, 16bit で録音したデータをビットレート 320kbps で mp3 ファイルにしたものを聴き比べてみてください．音質の劣化はほとんど気にならないと思います．ところがファイルの大きさは 1/5 以下になっているのです．

320kbps.mp3

MIDI

MIDI 形式は，上で説明してきたのとは全く別の符号化形式です．非常に粗っぽく言えば，MIDI 形式では「楽譜のデータ」のみを符号化します．また MIDI ファイルを再生する際には，それぞれの音の音色を格納した「MIDI 音源」と呼ばれるデータをコンピュータの中に予め用意しておき，MIDI ファイルに入っている楽譜を MIDI 音源に従って演奏するという方法で音を鳴らします．この方法ではやりとりされるのが楽譜データだけですから，ファイルサイズ自体は非常に小さくなります．